他のプログラムも
  智慧とデータが拓くエレクトロニクス新材料開発拠点　公開・非公開プログラム情報
で公開しています

Kronig-Penneyモデルによる１次元結晶の波動関数

プログラム kronig_penney.pyと本ページは、
シミュ君日記のYoutube動画がきっかけになって作成したものです

2024年度 結晶工学スクール 関連資料 で 公開しているkronig_penney.pyを使って作ったアニメーションです。

• アニメーションでは、固有関数の時間変化を表示しています。
  時間依存Schrödinger方程式から、固有関数の時間変化は \( \mathrm{exp}(-i E / \hbar) = \mathrm{exp}(-phase_{step} \cdot t) \) の位相項が掛かります。
  そのため、kronig_penney.py では、\( phase_{step} \)  が \( E(k_w) \) にだいたい比例するように、\( k_w^2 \) に比例させています。
  しかしながら、これはあくまでもわかりやすく視覚化するための対応であり、物理的に意味があるとは限らないことに注意してください。
  ・ Bloch波はBZ境界近傍より大きなk_wでは、干渉により波動関数が大きく変わります。
  　そのため、上記のエネルギー位相項と電子の速度に関係を見ることはできません。
  ・ 電子の速度は、波動関数の波束の速度として群速度 \( v_g(k) = d^2E(k) / dk^2 / \hbar \) で与えられるので、上記のエネルギー位相項とは関係ありません
  ・ エネルギーにはエネルギー原点の任意性があるため、上記のエネルギー位相の振動数にも任意性があります。
  　そのため、波動関数の絶対値としての振動を表していません。
  ・ 波の位相速度は  \( v_p = E(k) / (\hbar k) \) となりますが、この場合にもエネルギーの任意性が現れます。
  ・ Γ点のエネルギー (最低エネルギー) を原点にとったうえで、Γ点近傍では、位相速度と群速度が一致します。
  　そのため、アニメーションで見られる位相の移動速度は、電子の移動速度とみなしても大きな誤解はないと思います。
  　この場合、Γ点では振動数が 0 になりますが、kronig_penney.py では視覚化のため、 \( phase_{step} \) に定数を設定しています。
• Bloch波数 k_w は\( 2\pi / a \)を単位とする部分座標です。
  k_w = 0 がΓ点、0.5 が ブリルアン・ゾーン (BZ) 境界 X点です。
  BZは 整数の Δk_w に対して周期性をもつということになります。

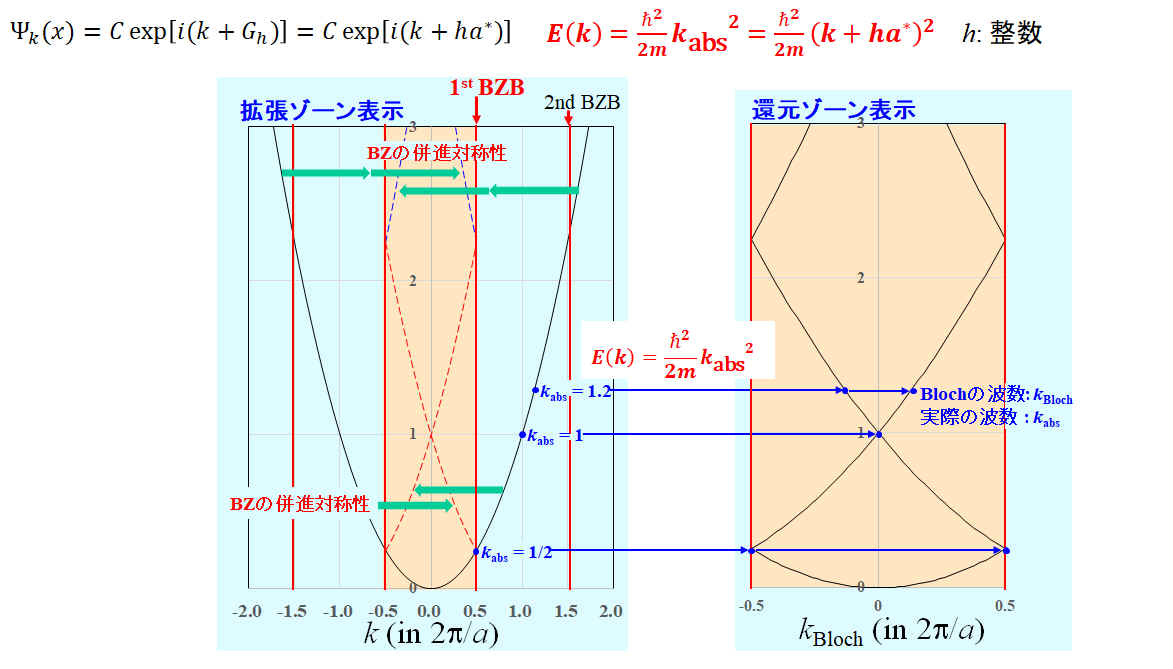
下図の拡張ゾーン表示と還元ゾーン表示を理解して、以下のアニメーションとBlochの波数ベクトルkwの関係を考えてみましょう。
より詳しい内容は BlochsTheorem.pdf を参照のこと

プログラム kronig_penney.py

Update:

• 2025/02/20 以下の修正を行いました
  ・ kw が [-1/2, 1/2] を超える範囲の場合、準位番号 iLevel を修正した波動関数を表示するようにした
  ・ 定常状態の固有関数に関する時間変化項 \( \mathrm{exp}(-i E / \hbar) \)に対応して、位相を \( k_w^2 \) に比例するように変更
• 2025/02/20 アニメーション機能を追加しました

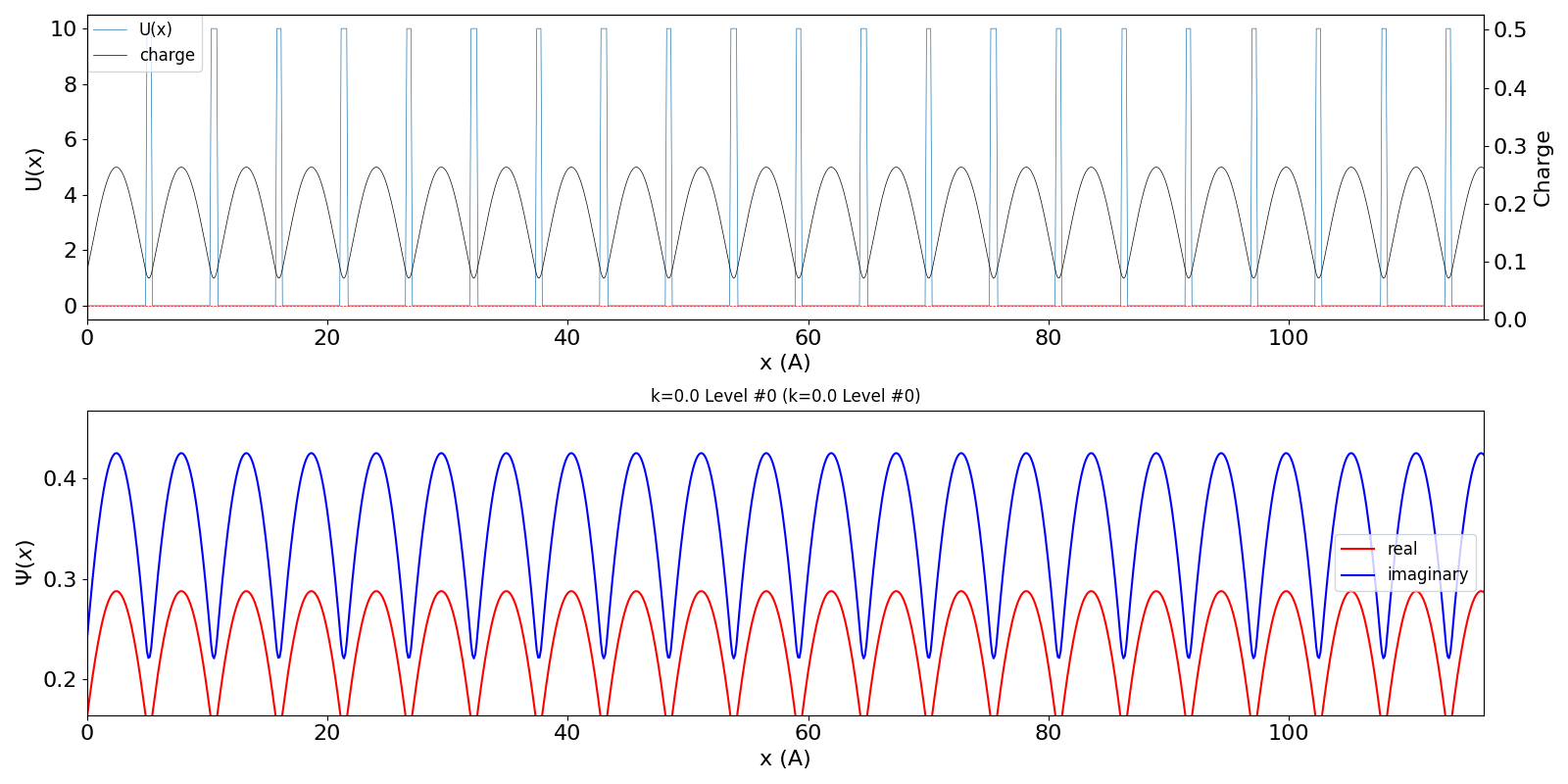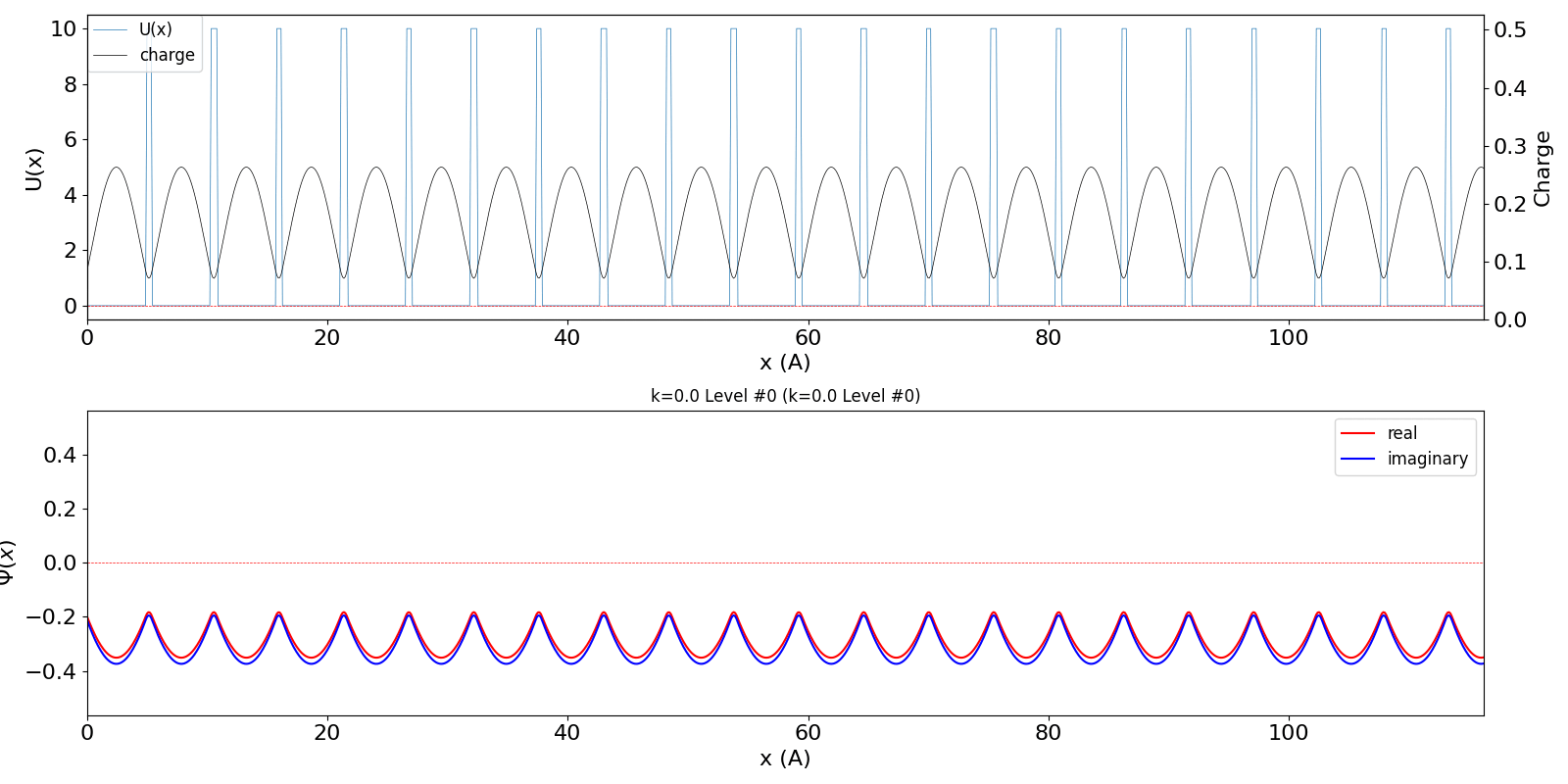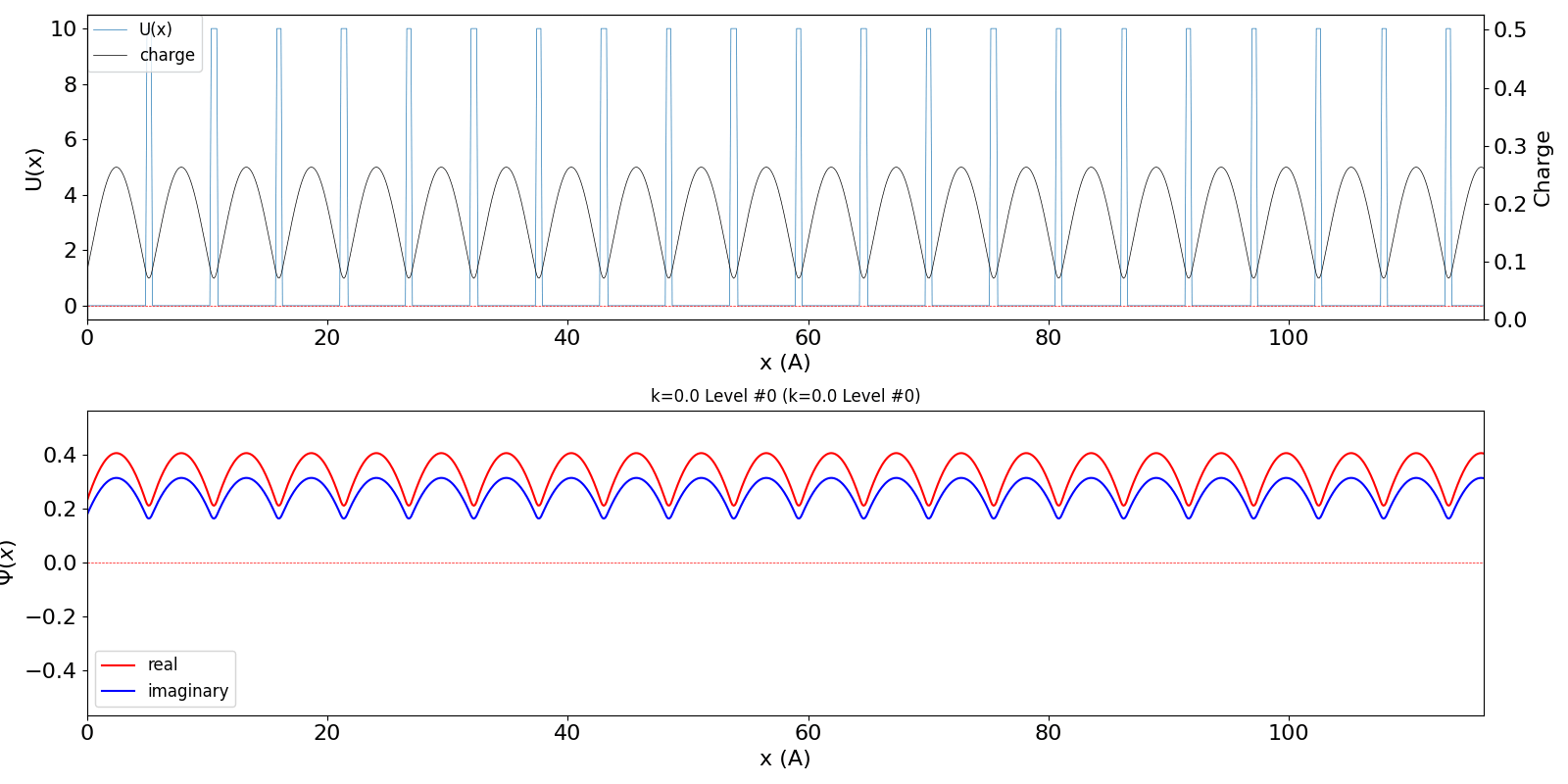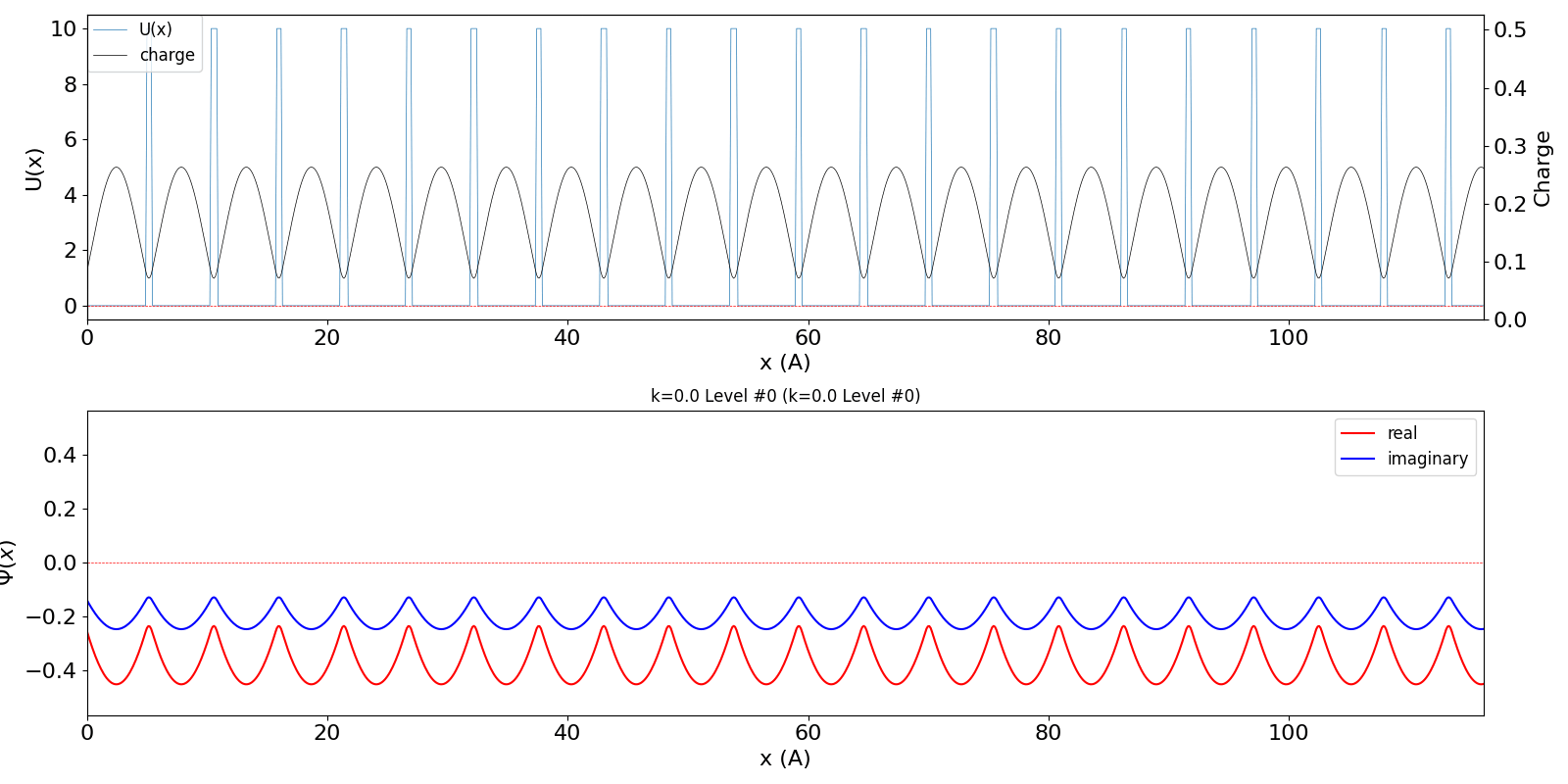
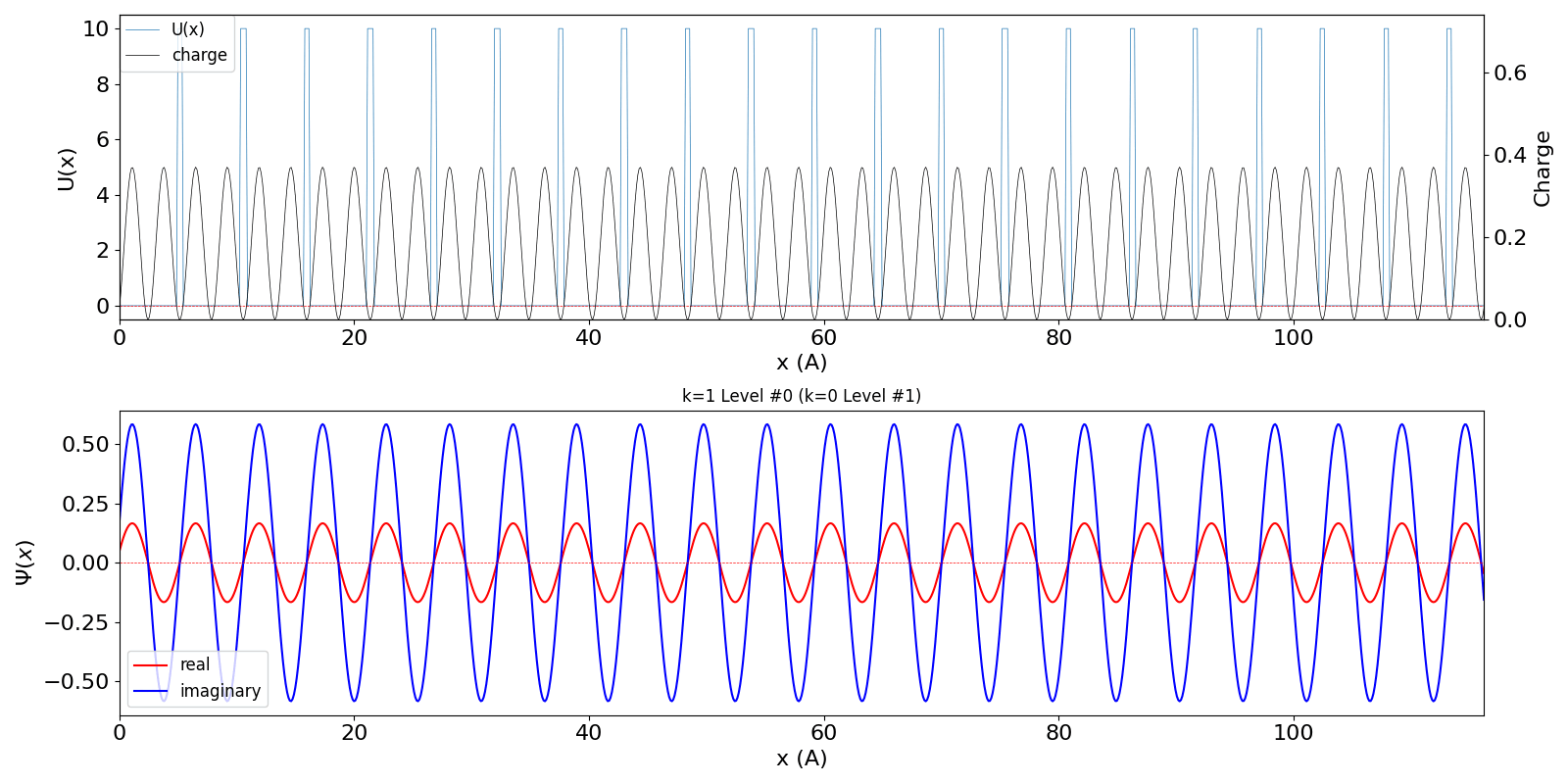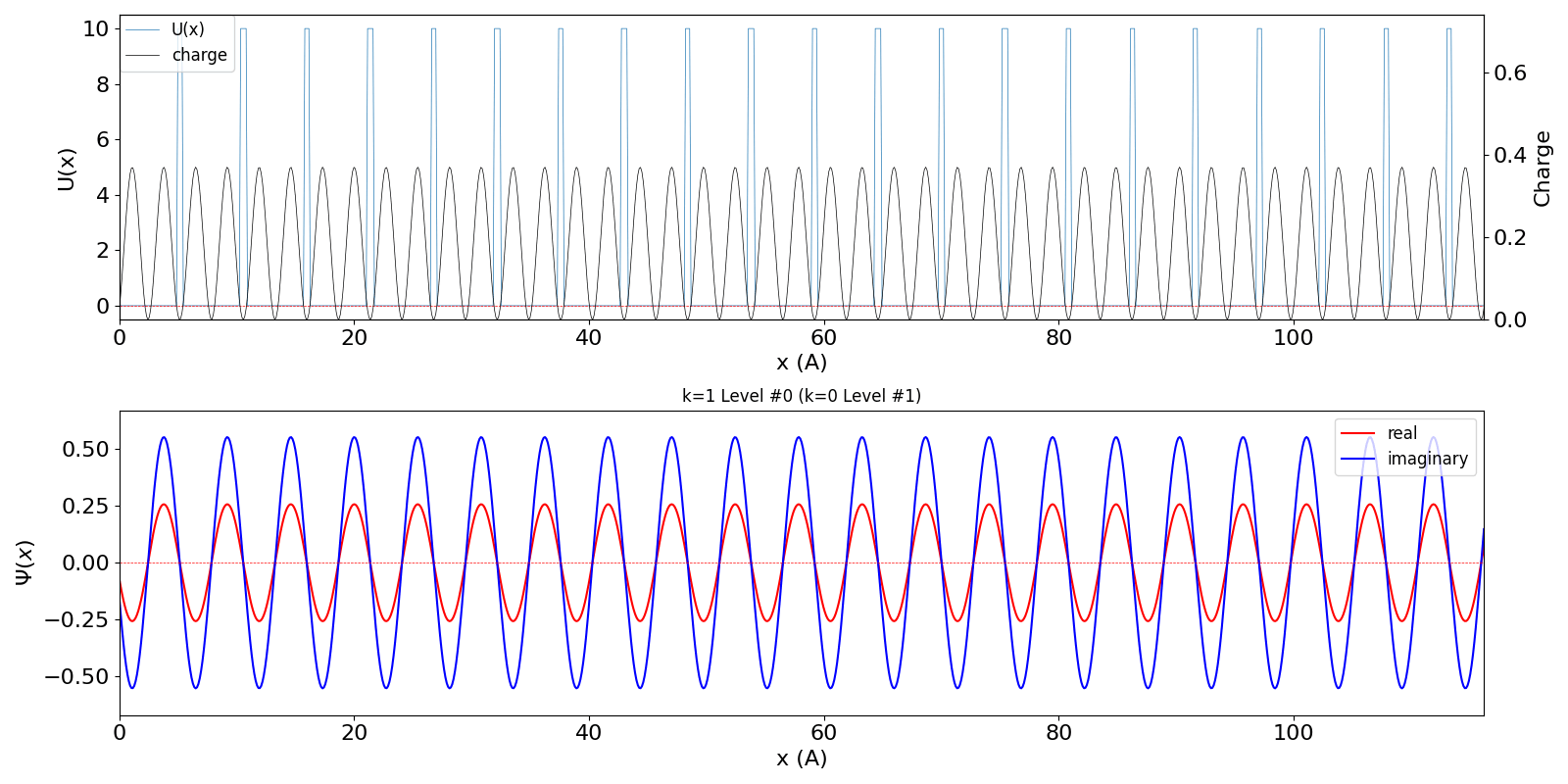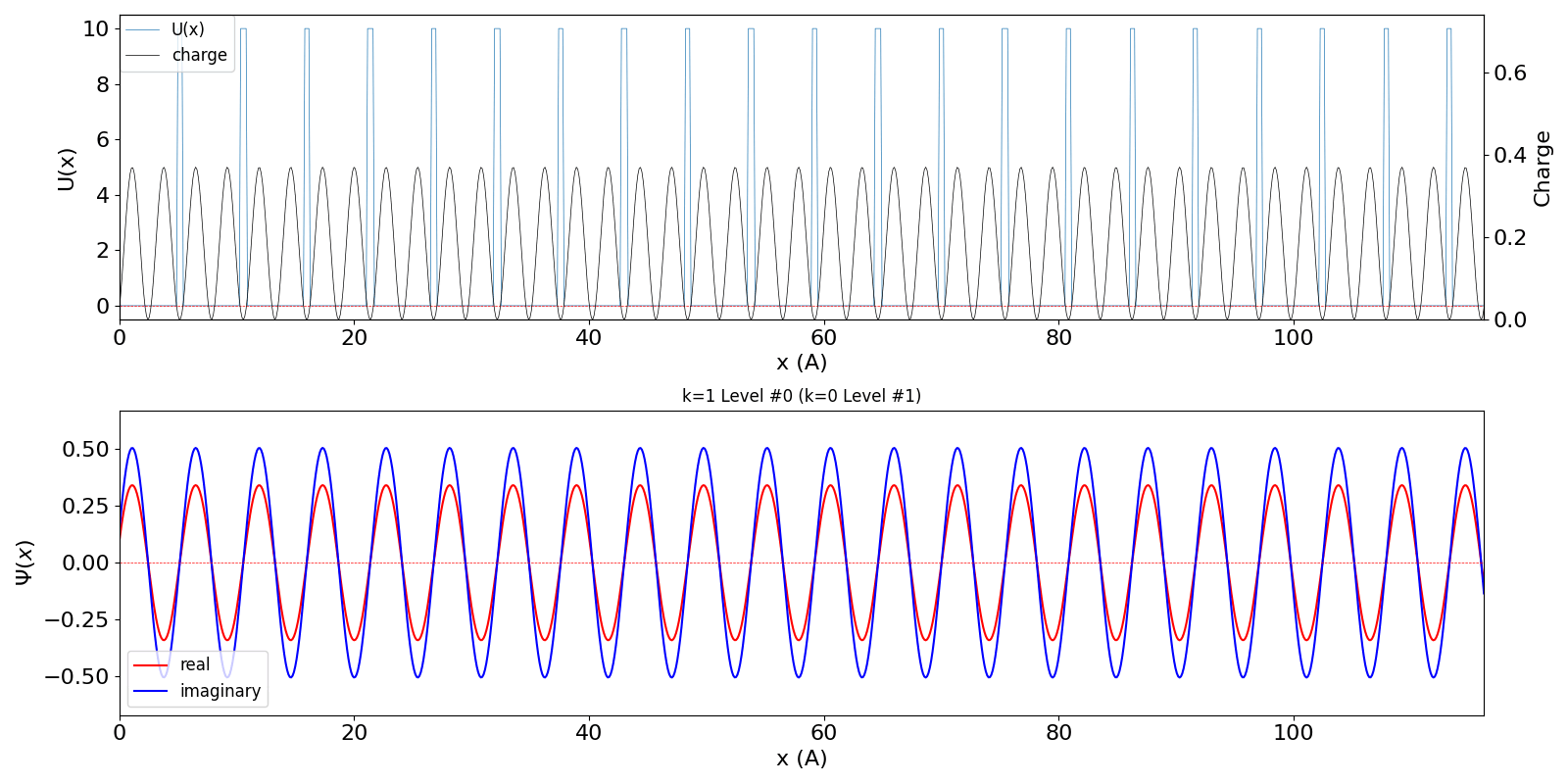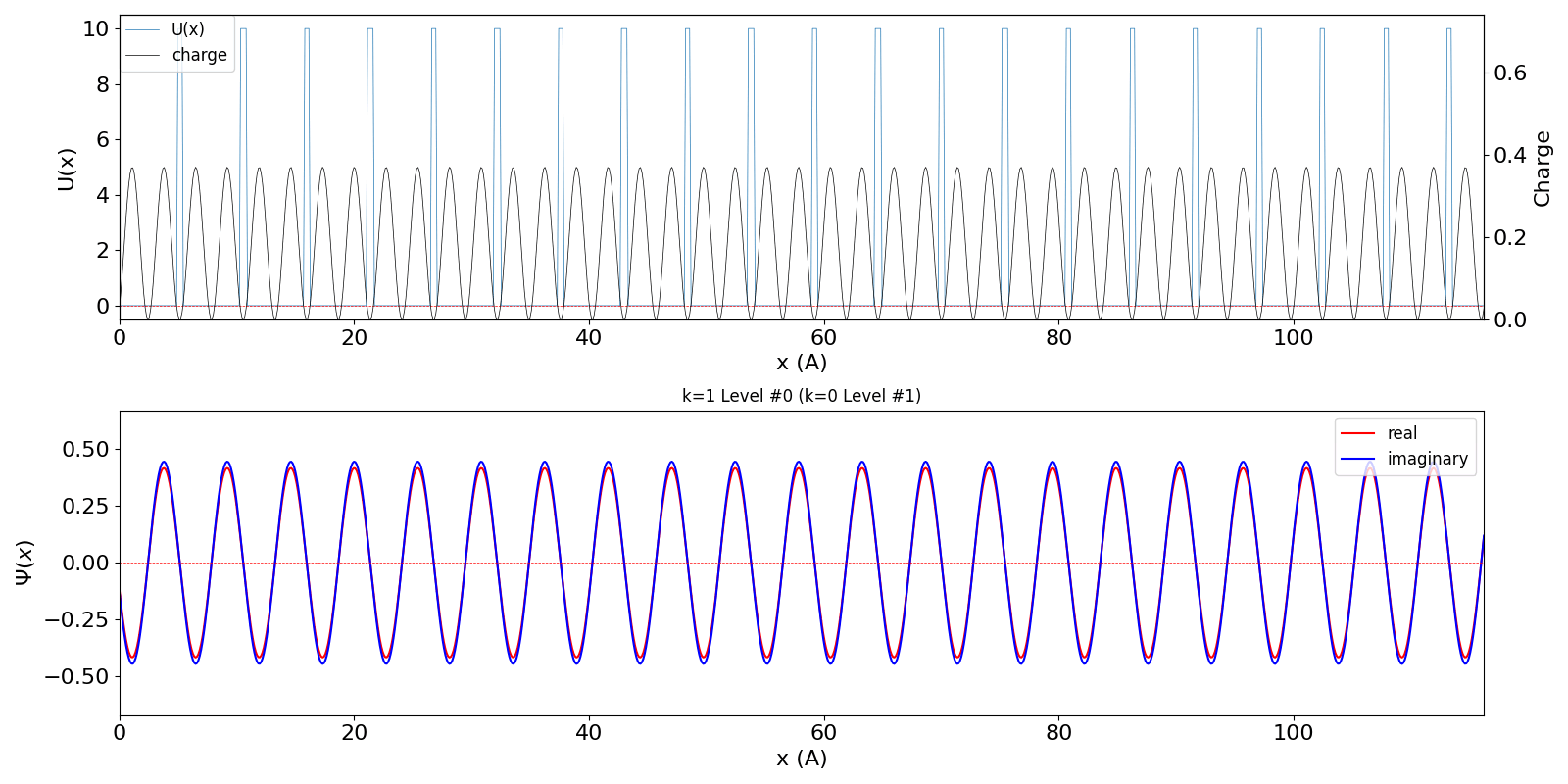
kw = 0 (Γ点) の波動関数 (左図) は、Bloch波の位相 (包絡線) は移動せず、位相 (実部と虚部の値) だけが時間変化します。 包絡線が移動しないので、速度は 0 ということになります。 第2準位 (iLevel = 1) (中図) は、BZ の周期性から、kw = 1.0 の波数の波動関数 (右図) に対応しています。 (厳密には、kw = 0, ±1, ±2, ・・・  の波動関数は kw = 0, ±1, ±2, ・・・ の波動関数と混成します。 より正確な計算を行う場合は、2024年度 結晶工学スクール 関連資料 で公開している平面波法のプログラム pw1.py をご覧ください)
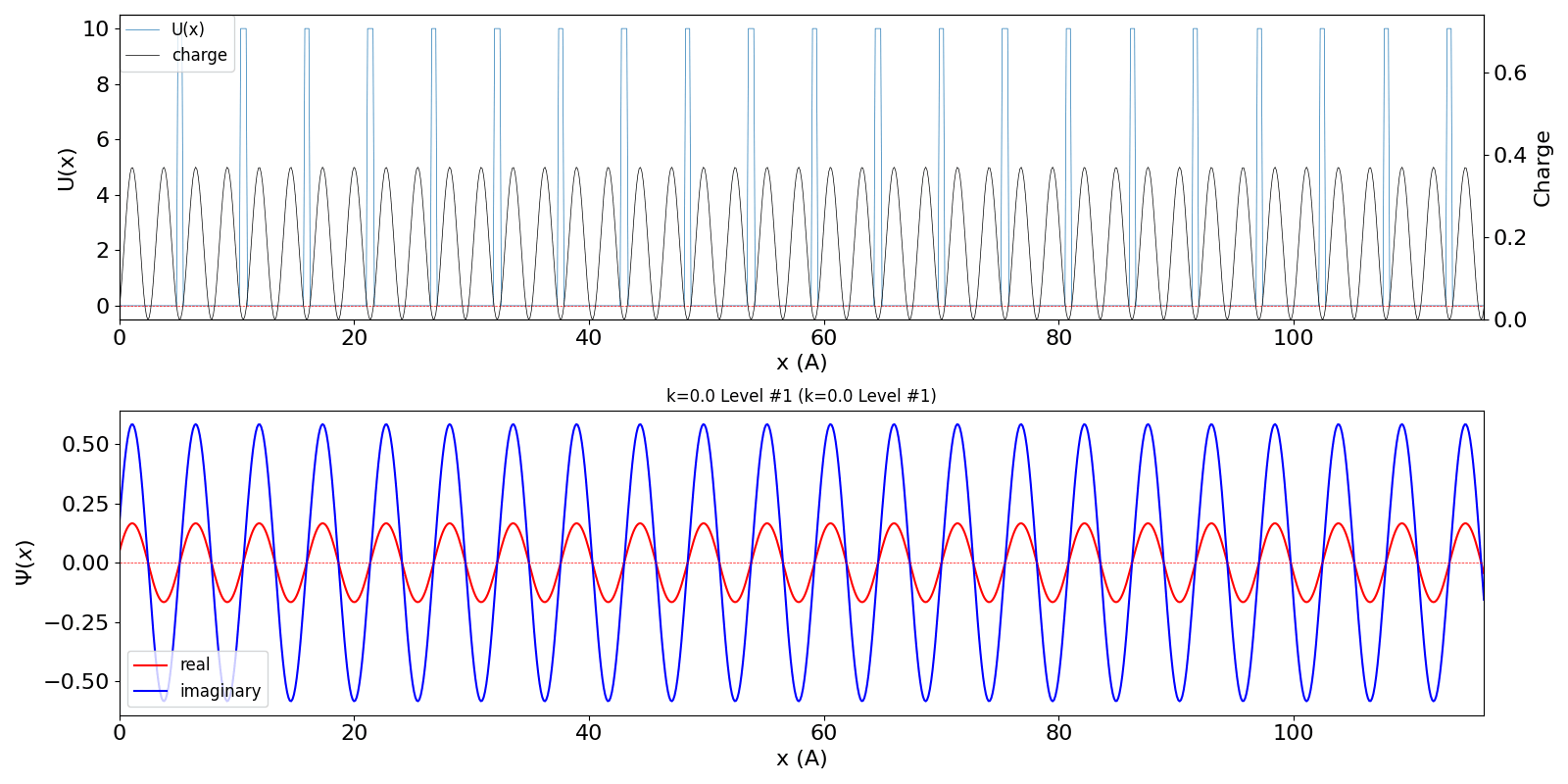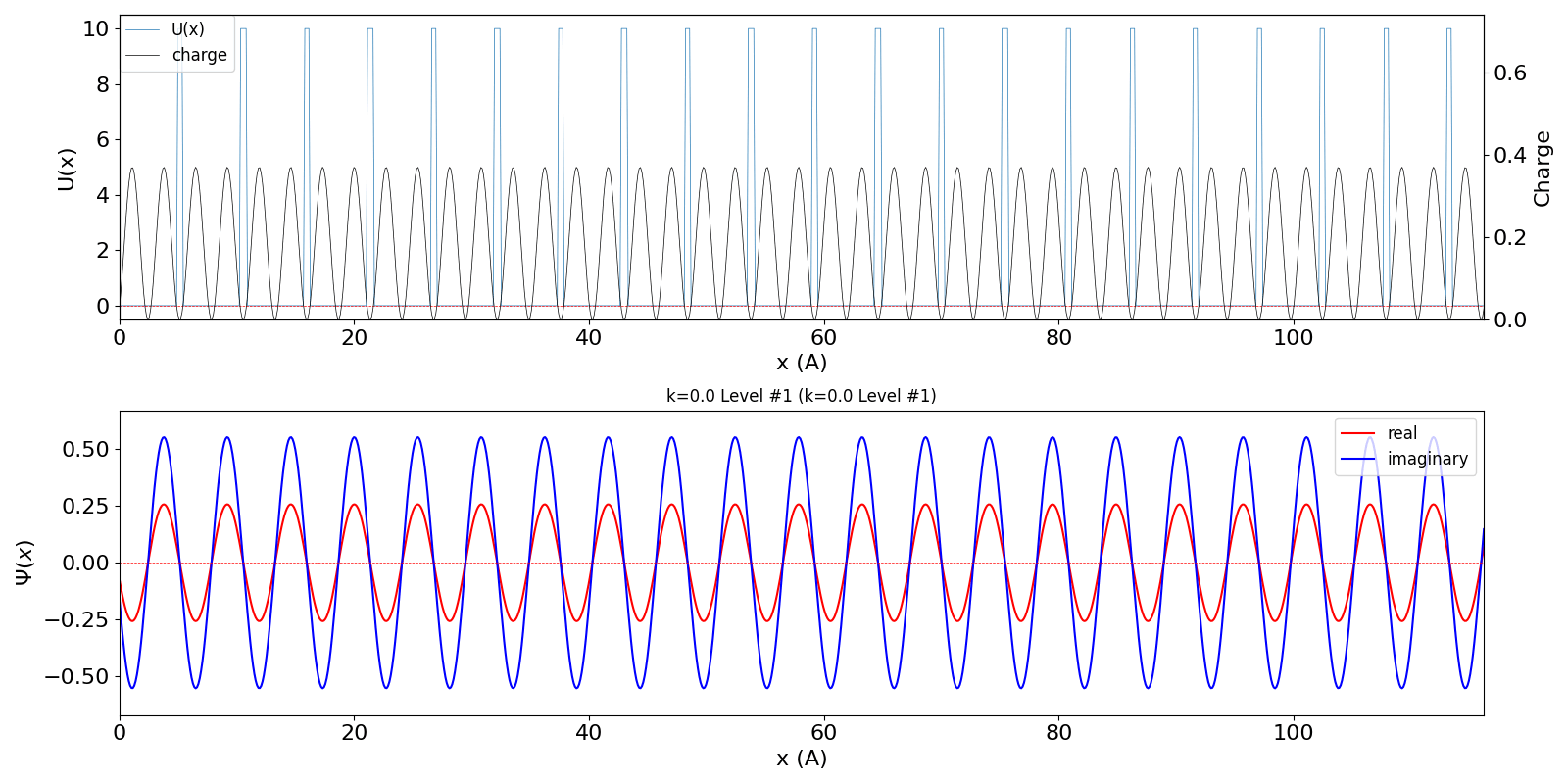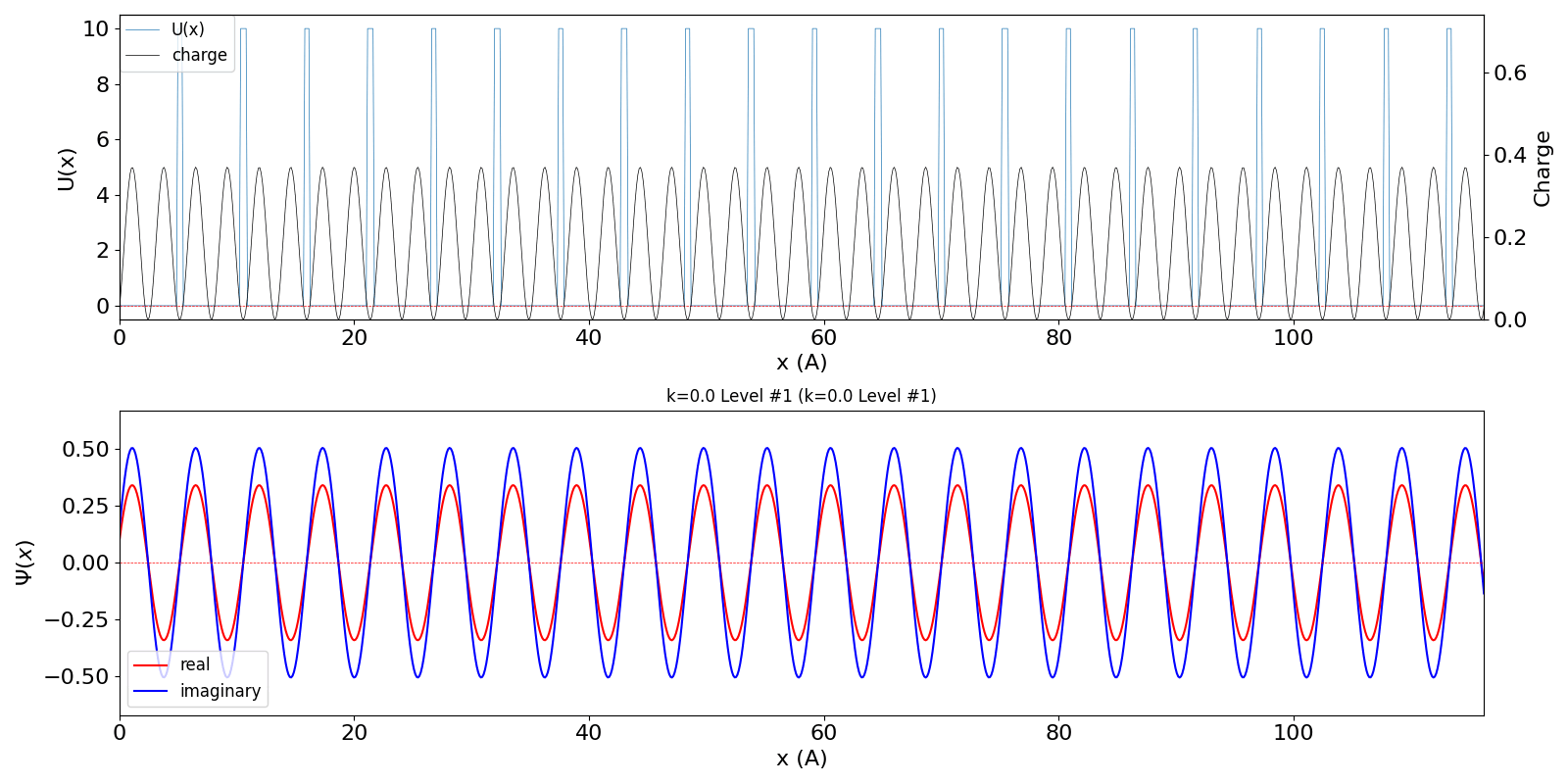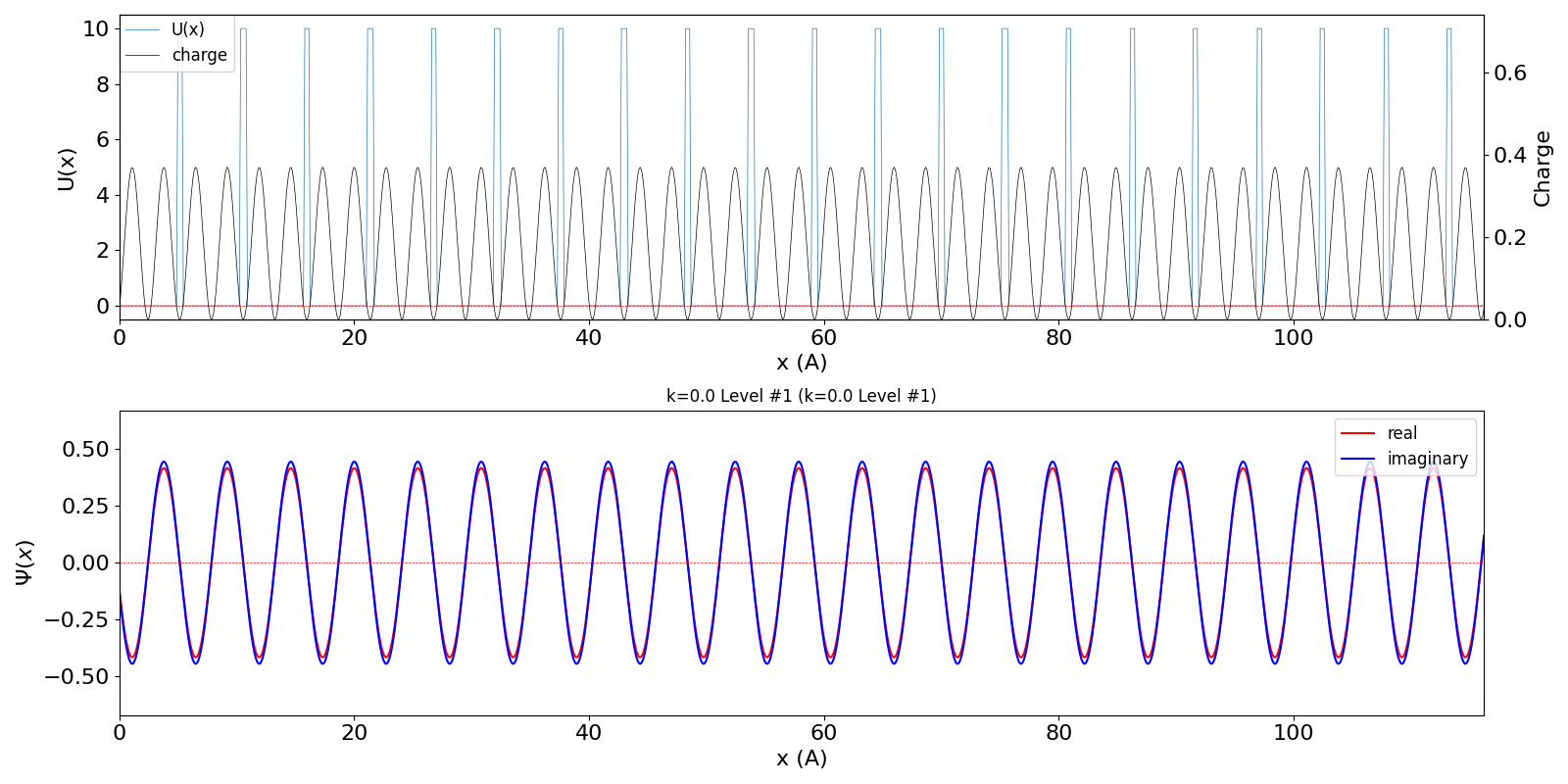
kronig_penney_wfanim_kw_0_Level_0.gif	kronig_penney_wfanim_kw_0_Level_1.gif	kronig_penney_wfanim_kw_1_Level_0.gif
kw = 0.03 になると、わずかですが、包絡線は右方向に移動しています。電子が右方向の速度と運動量を持っていることに対応しています。
kronig_penney_wfanim_kw_0.03_Level_0.gif
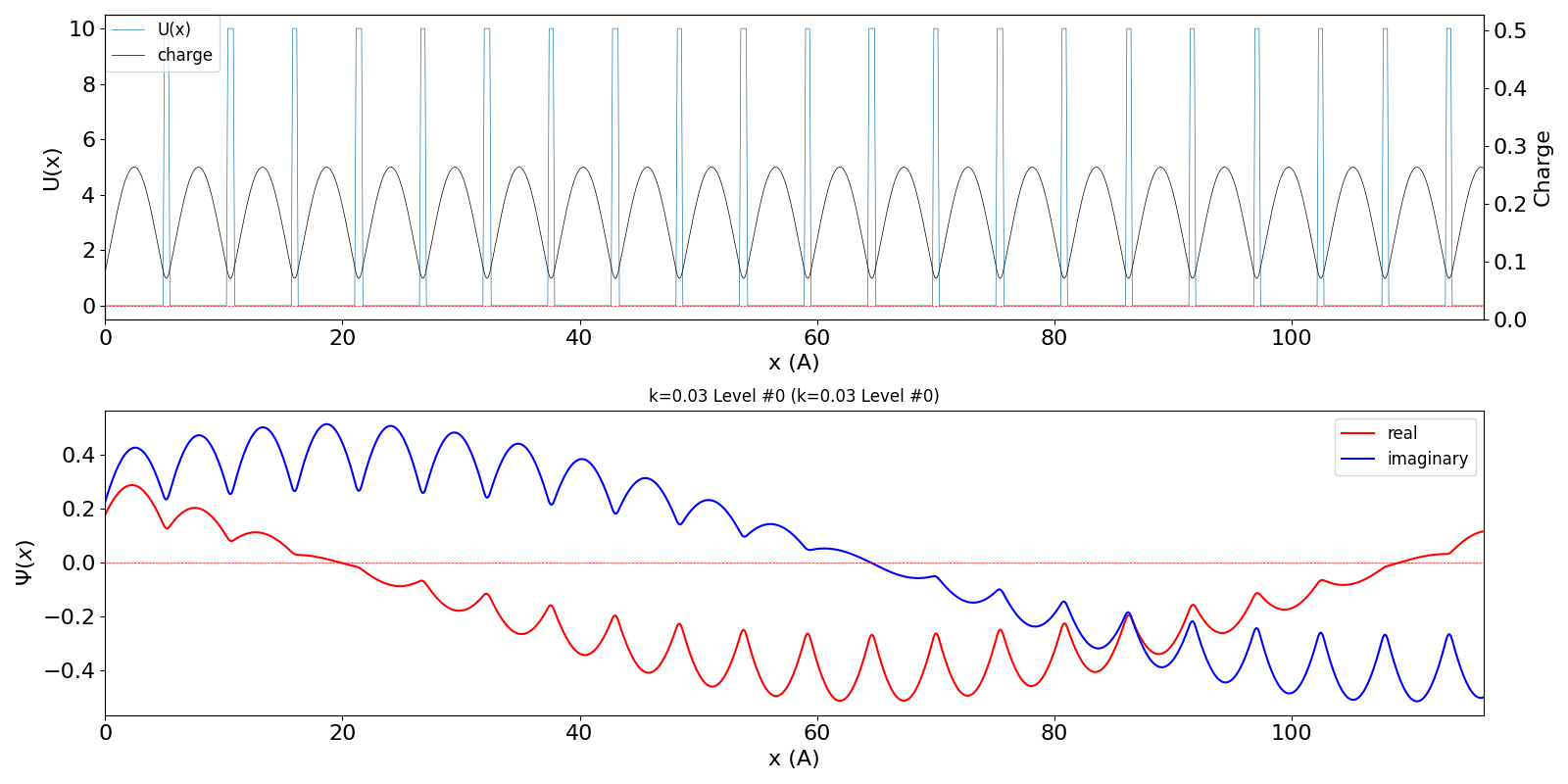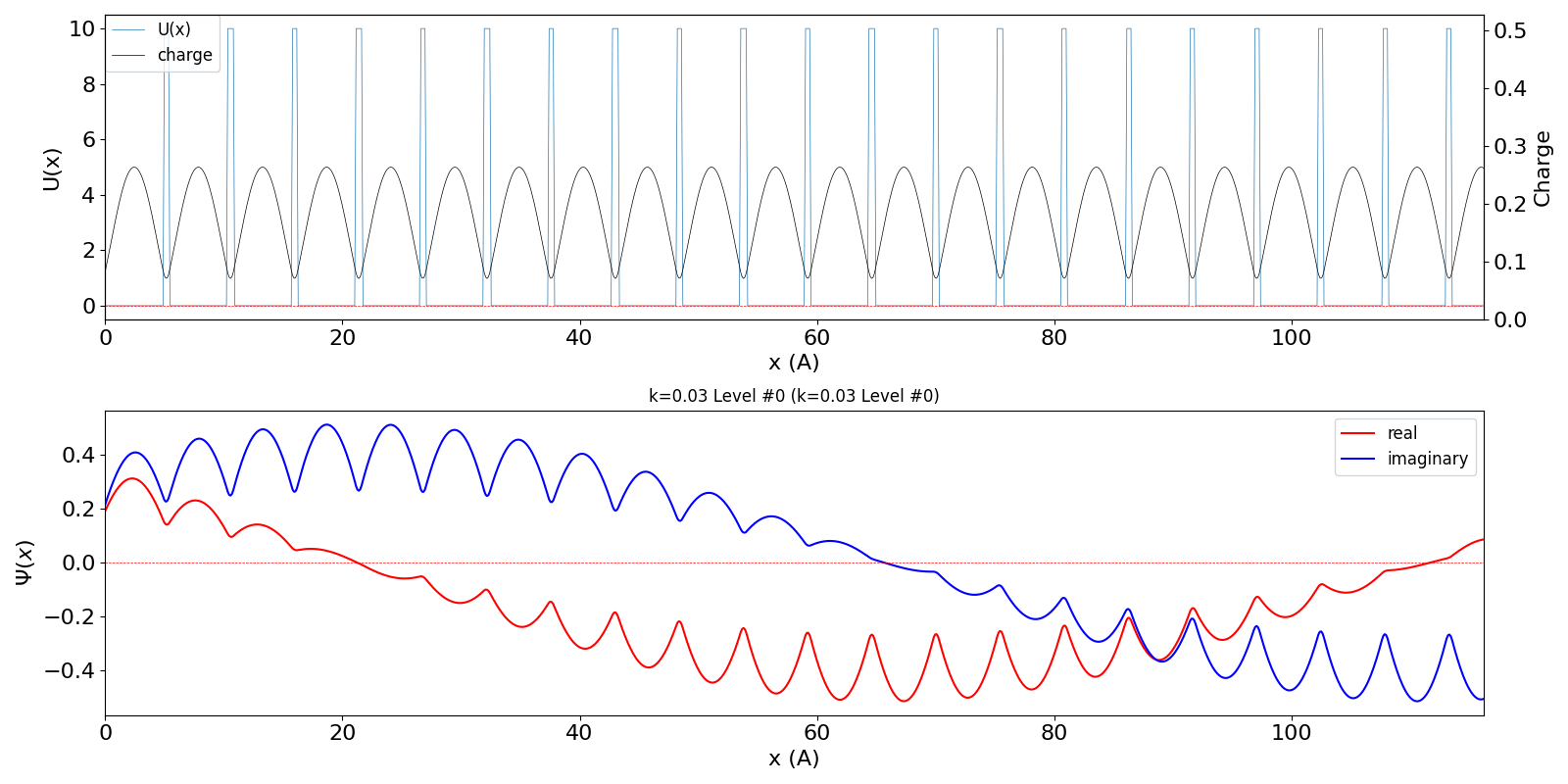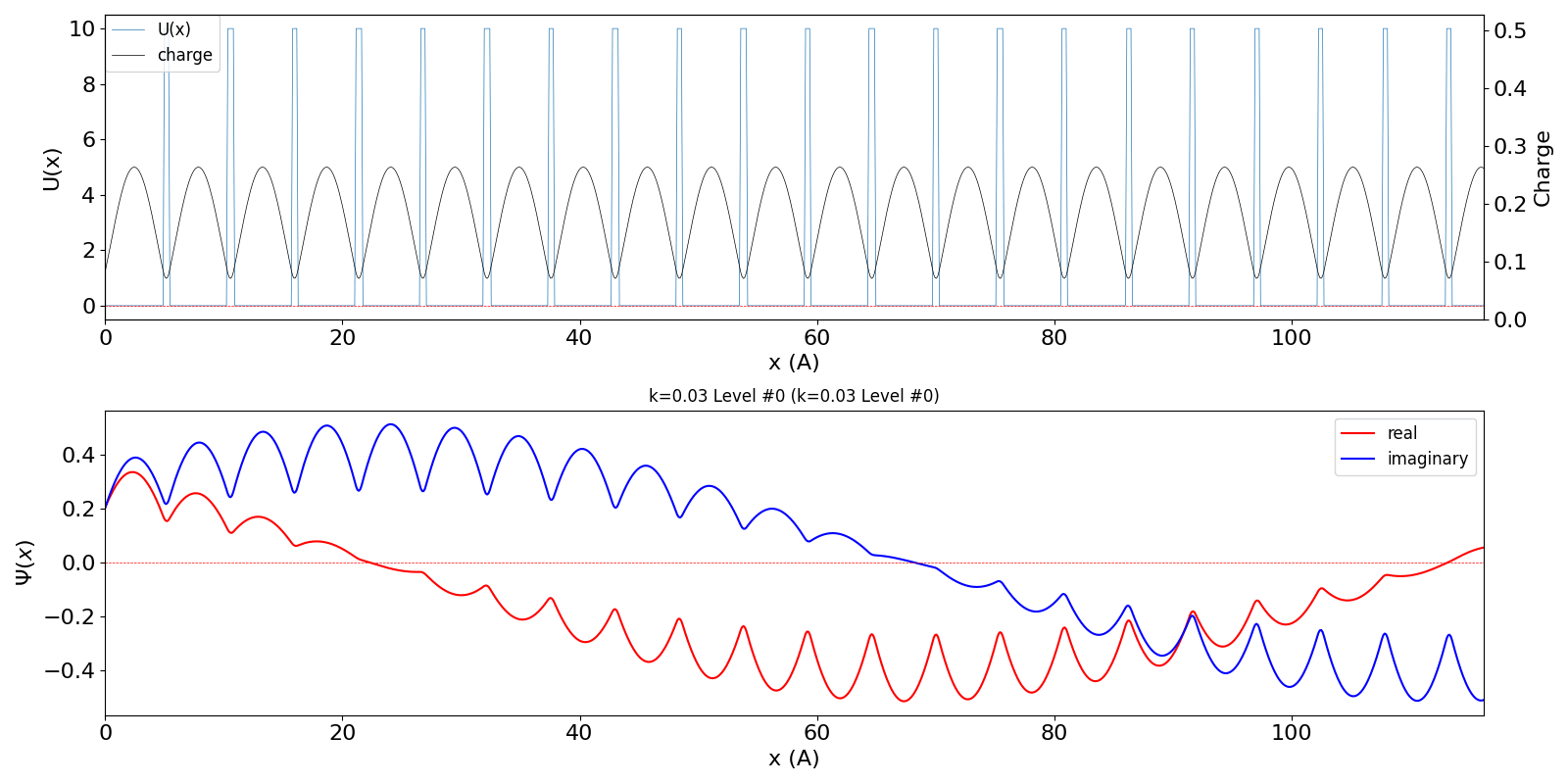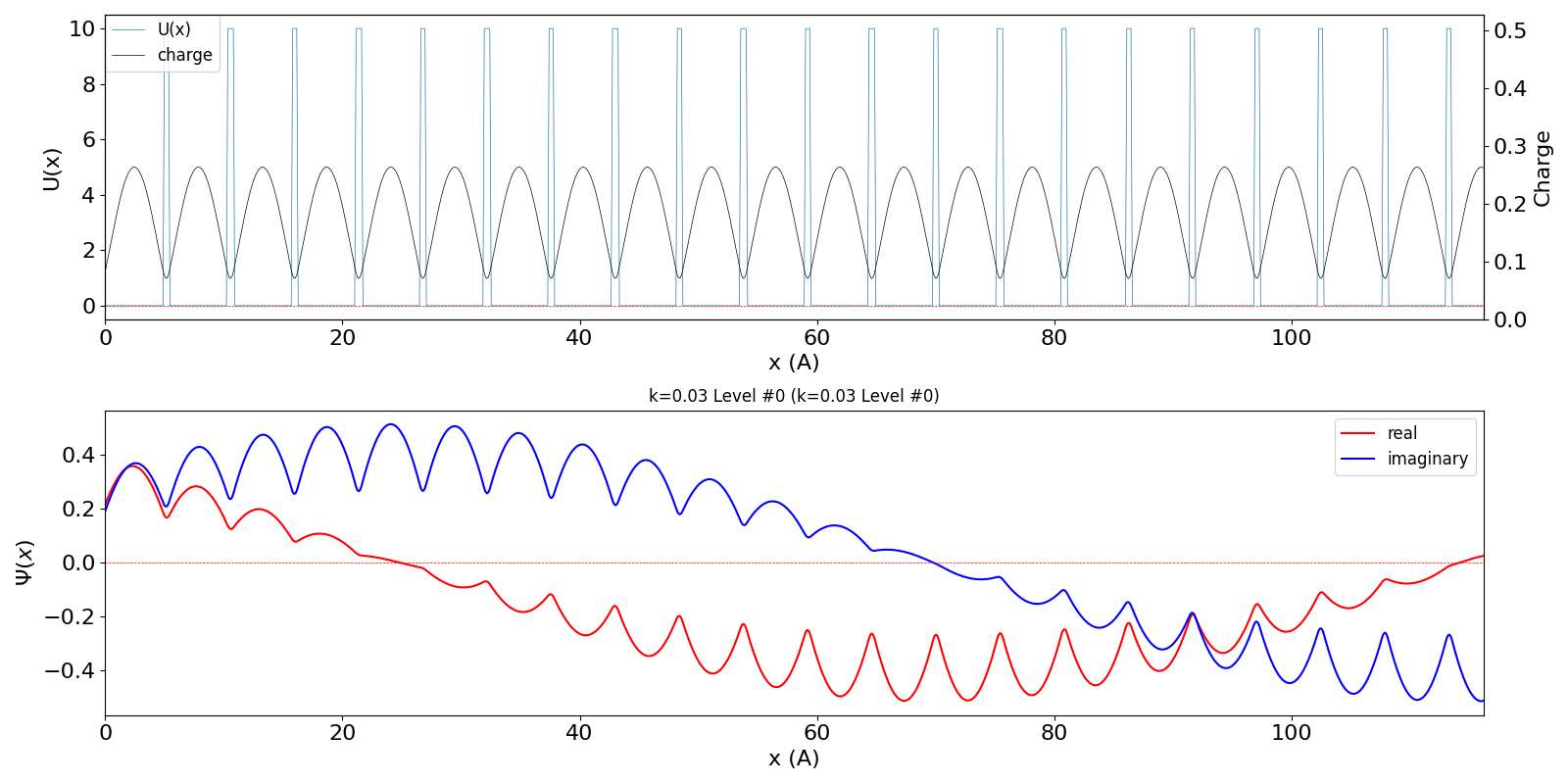
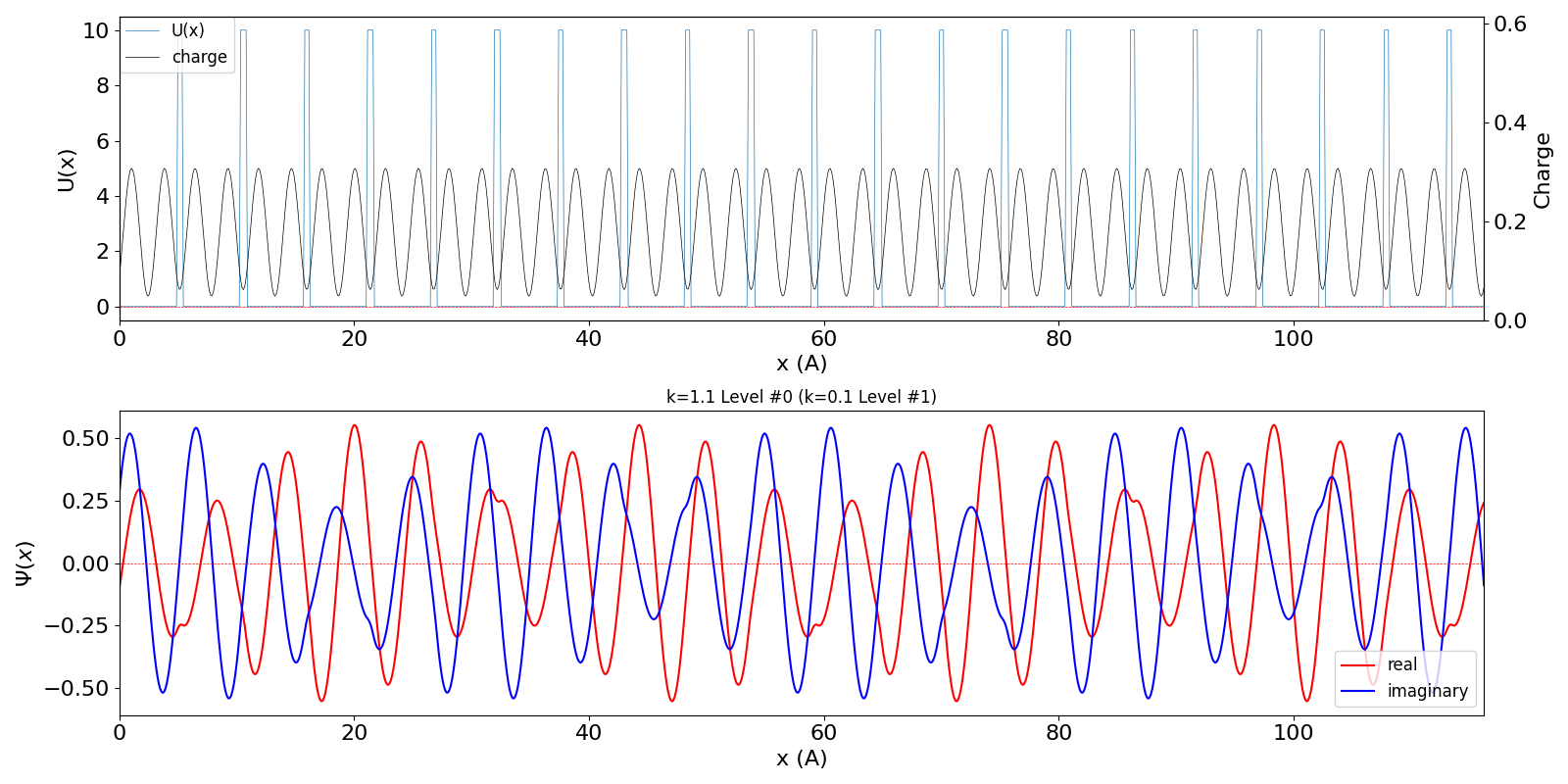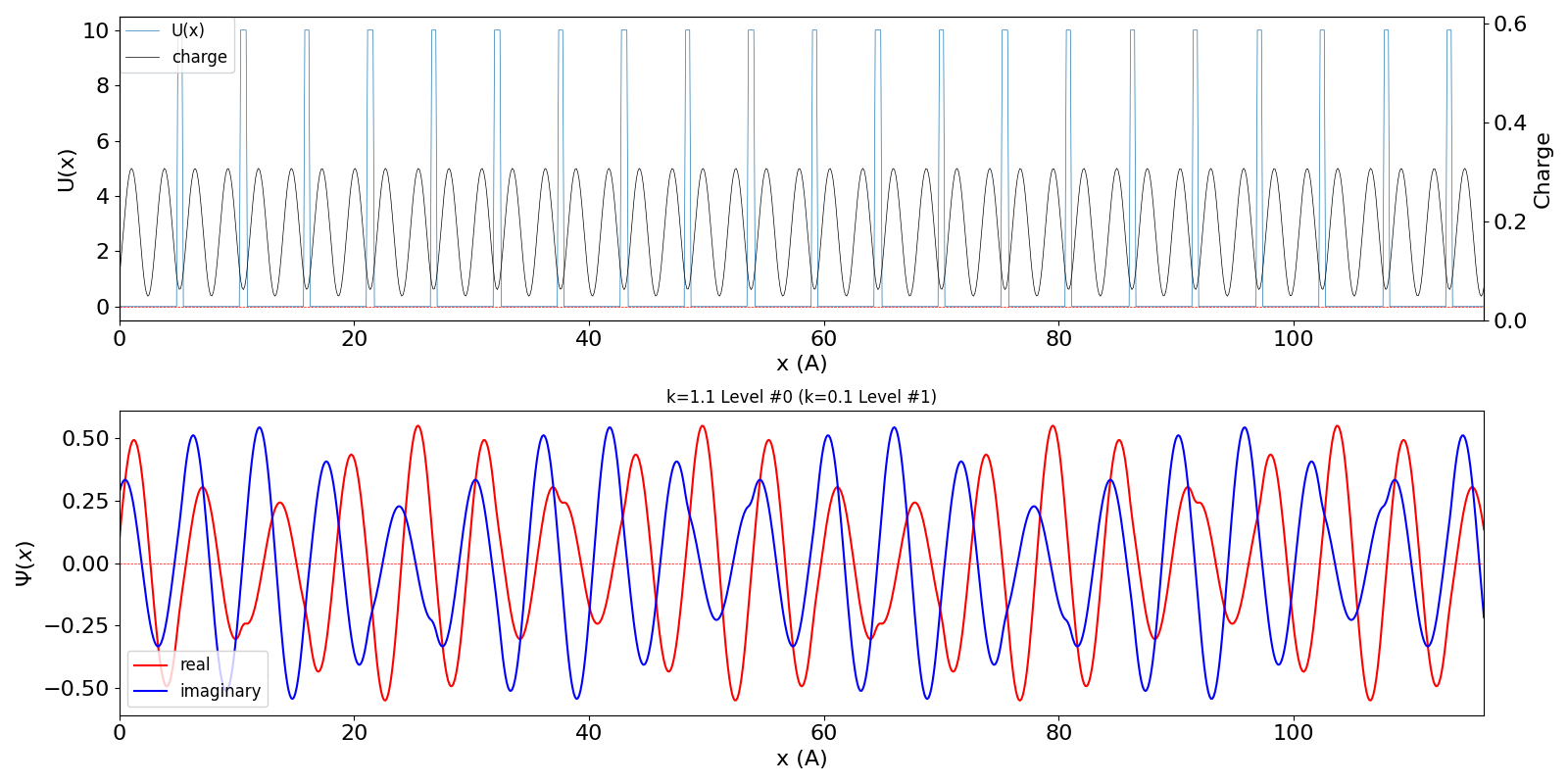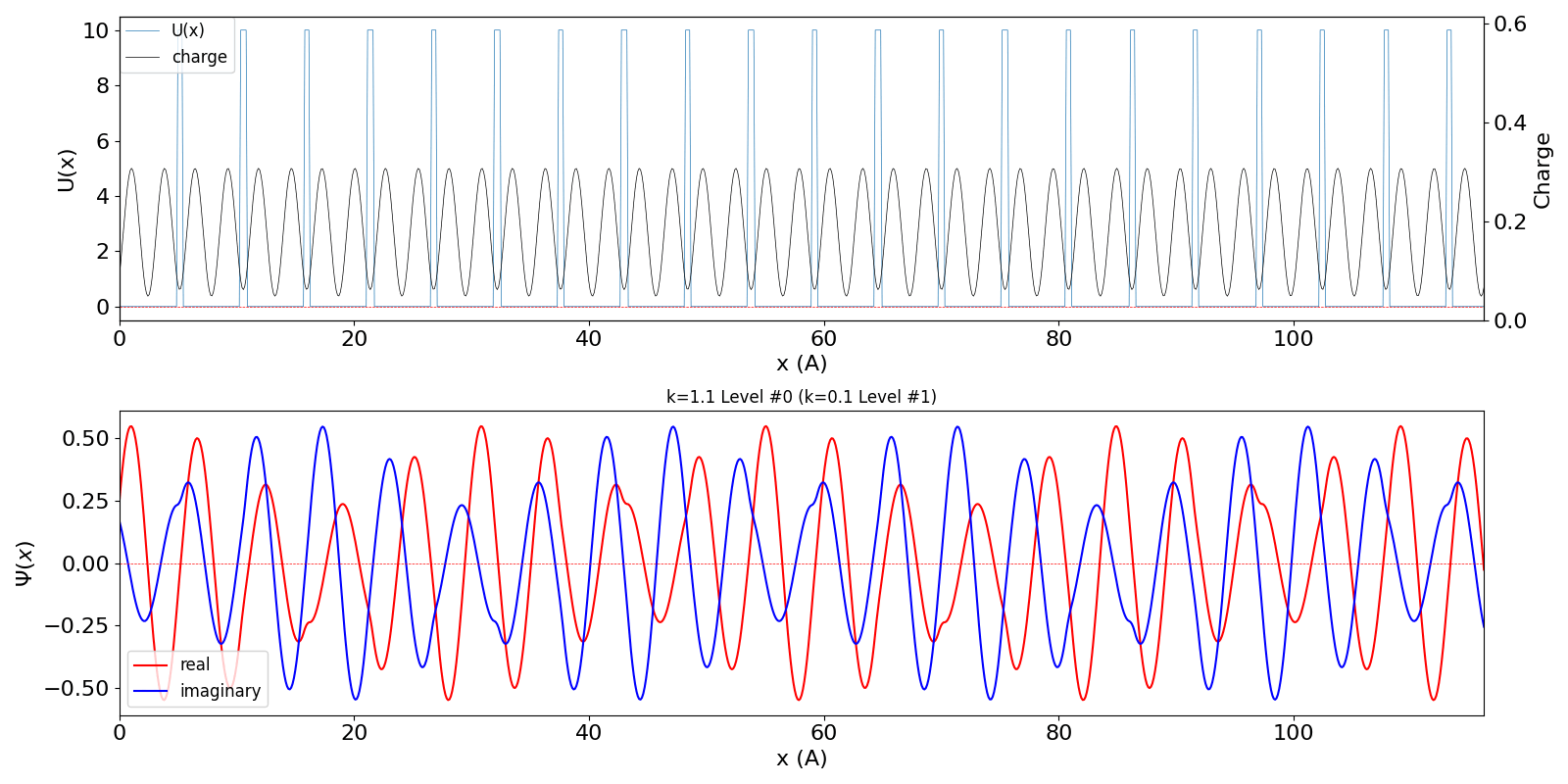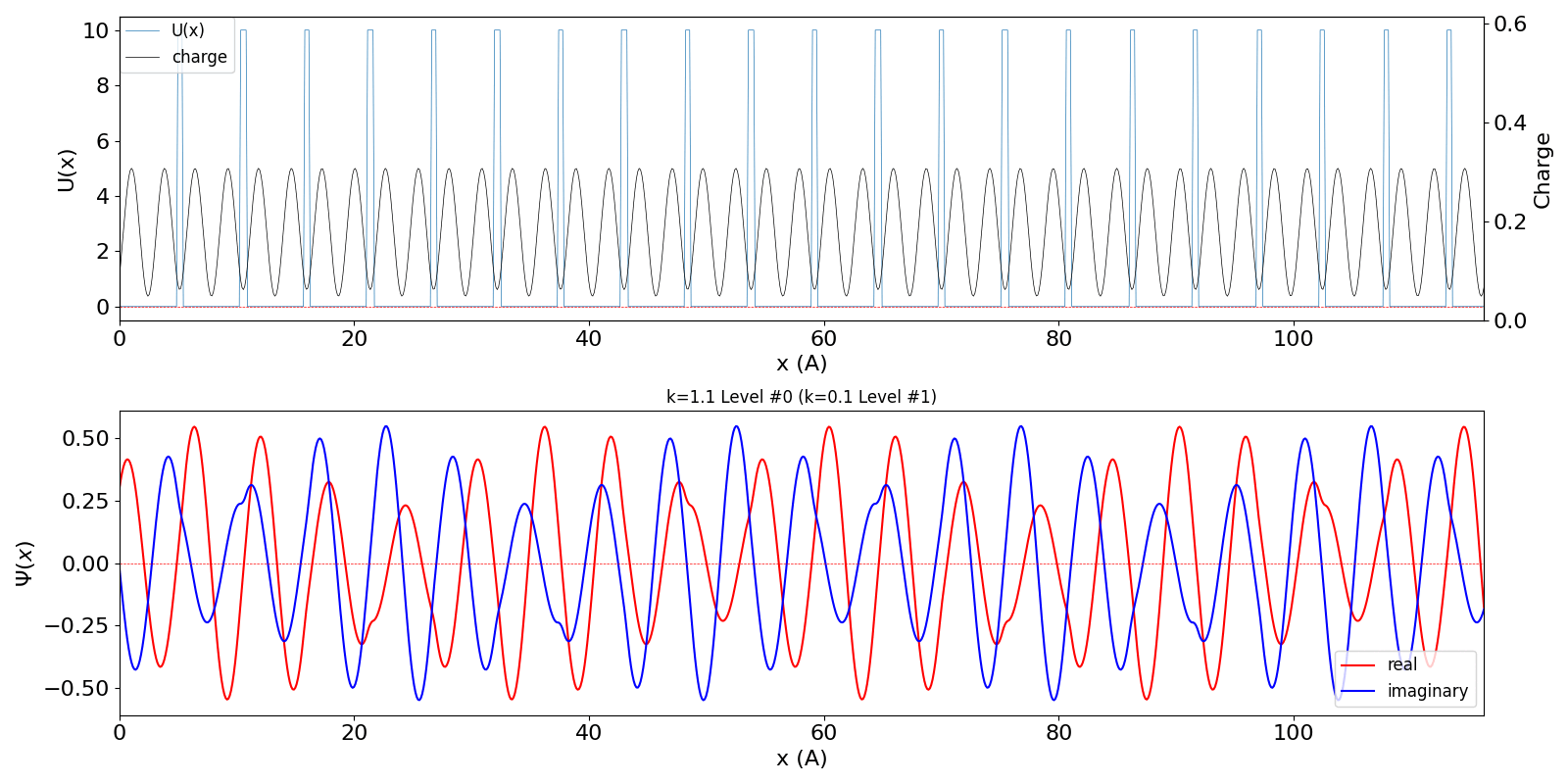
kw = 0.1 (左図) になると、包絡線が移動する速度が速くなります。電子の群速度が速くなっていることに対応しています。 kw = 1.1 の波動関数 (中図) は、kw = 0.1 の第2準位 (右図) に対応しています。
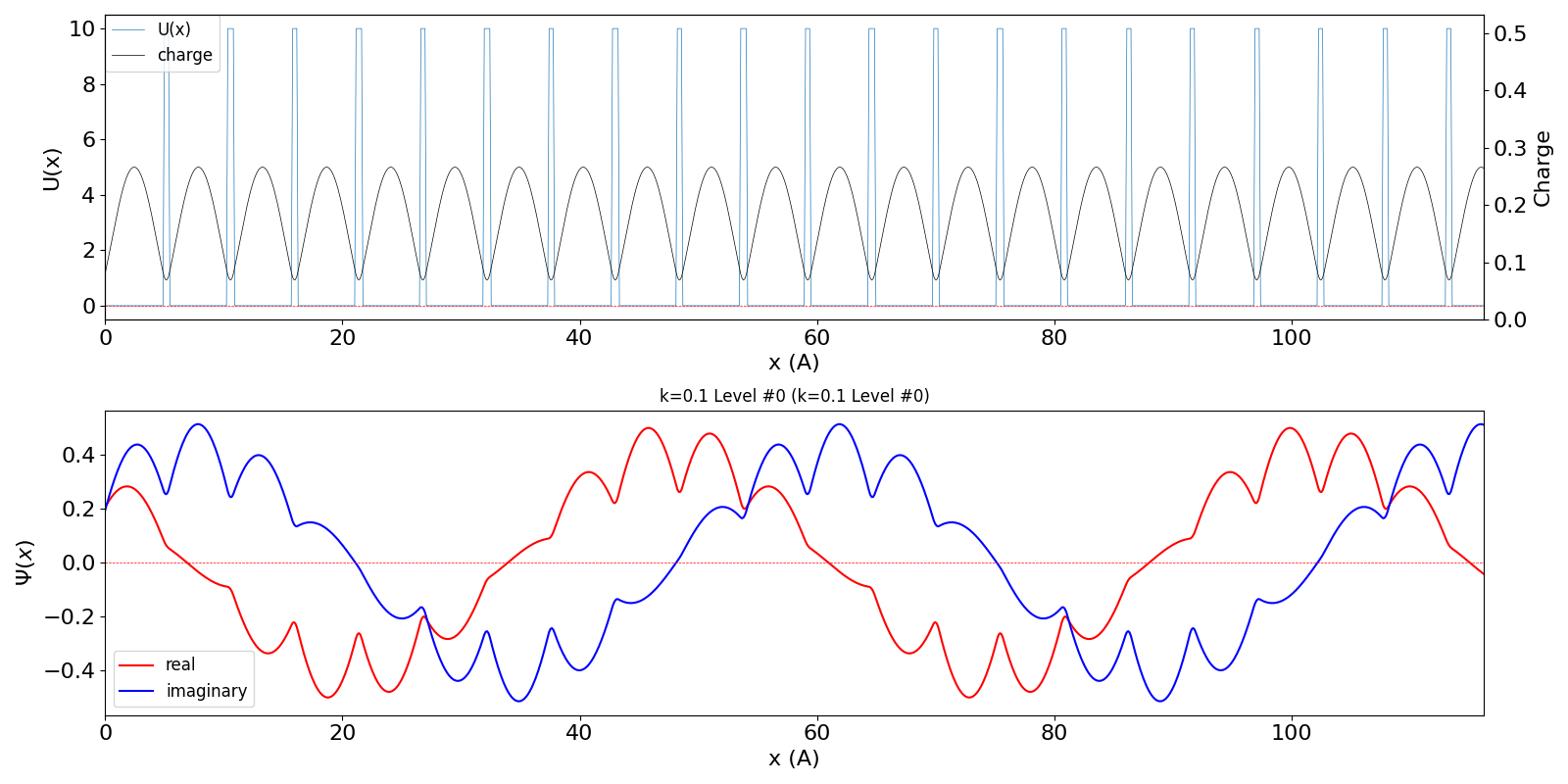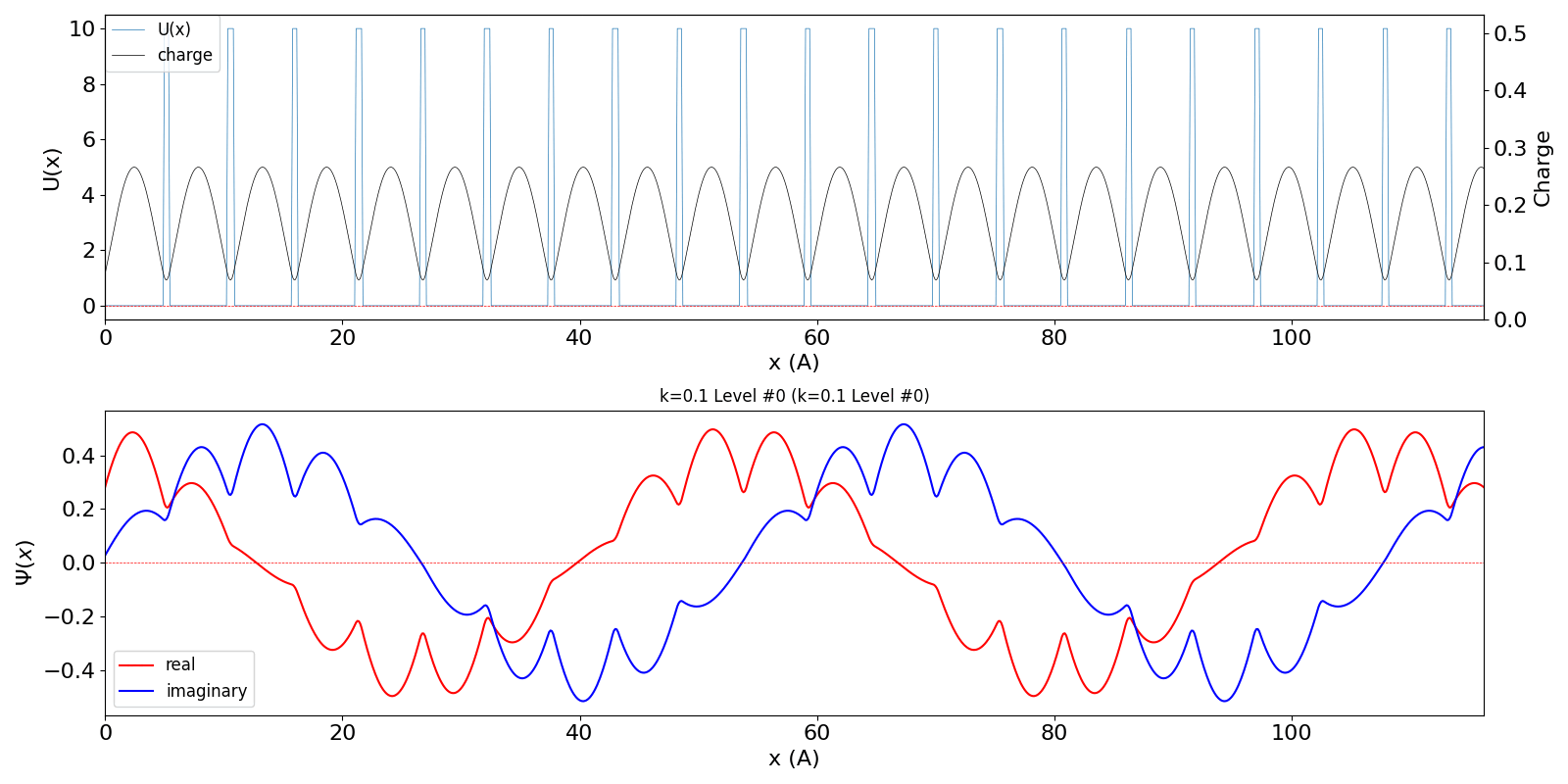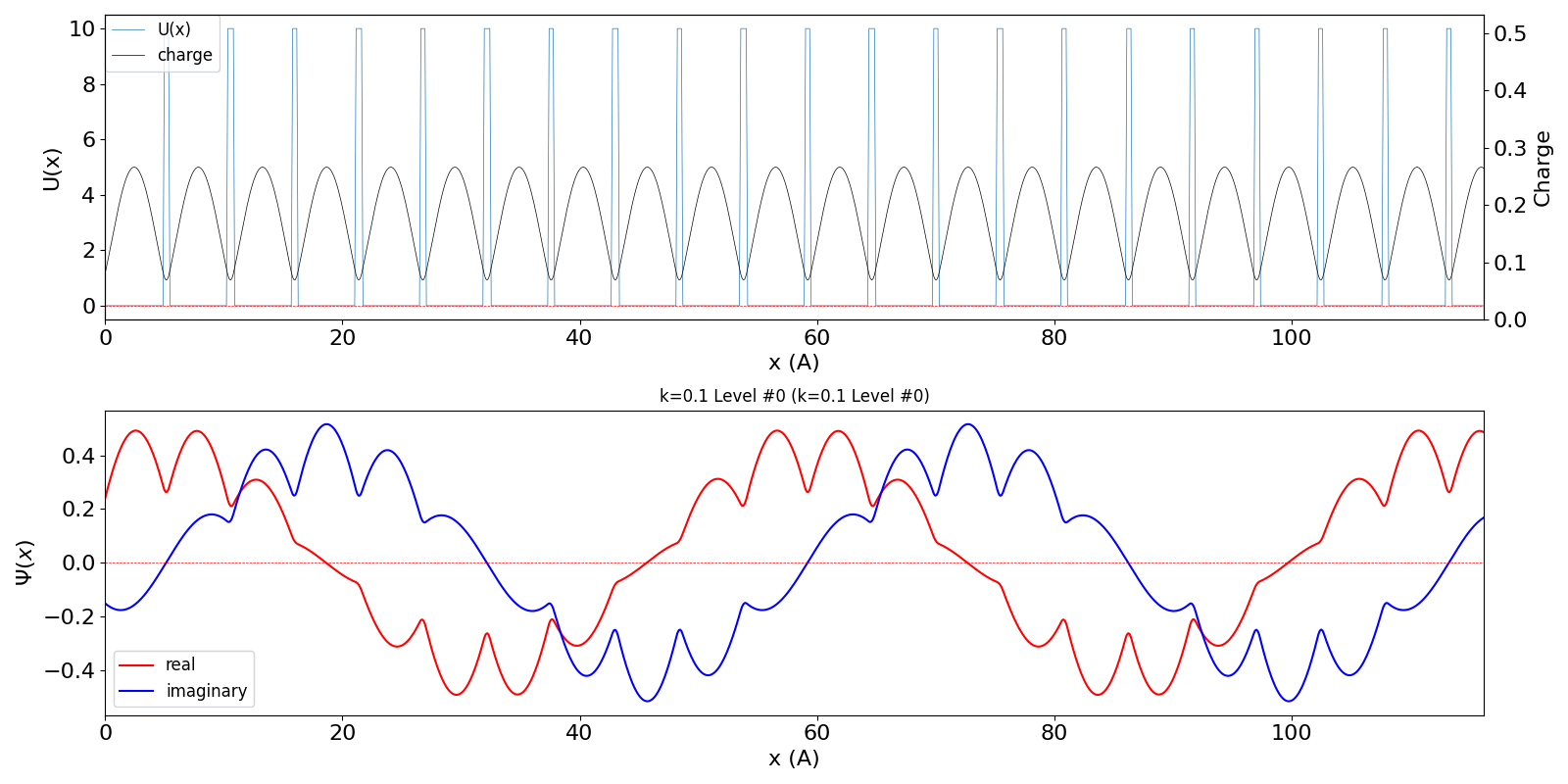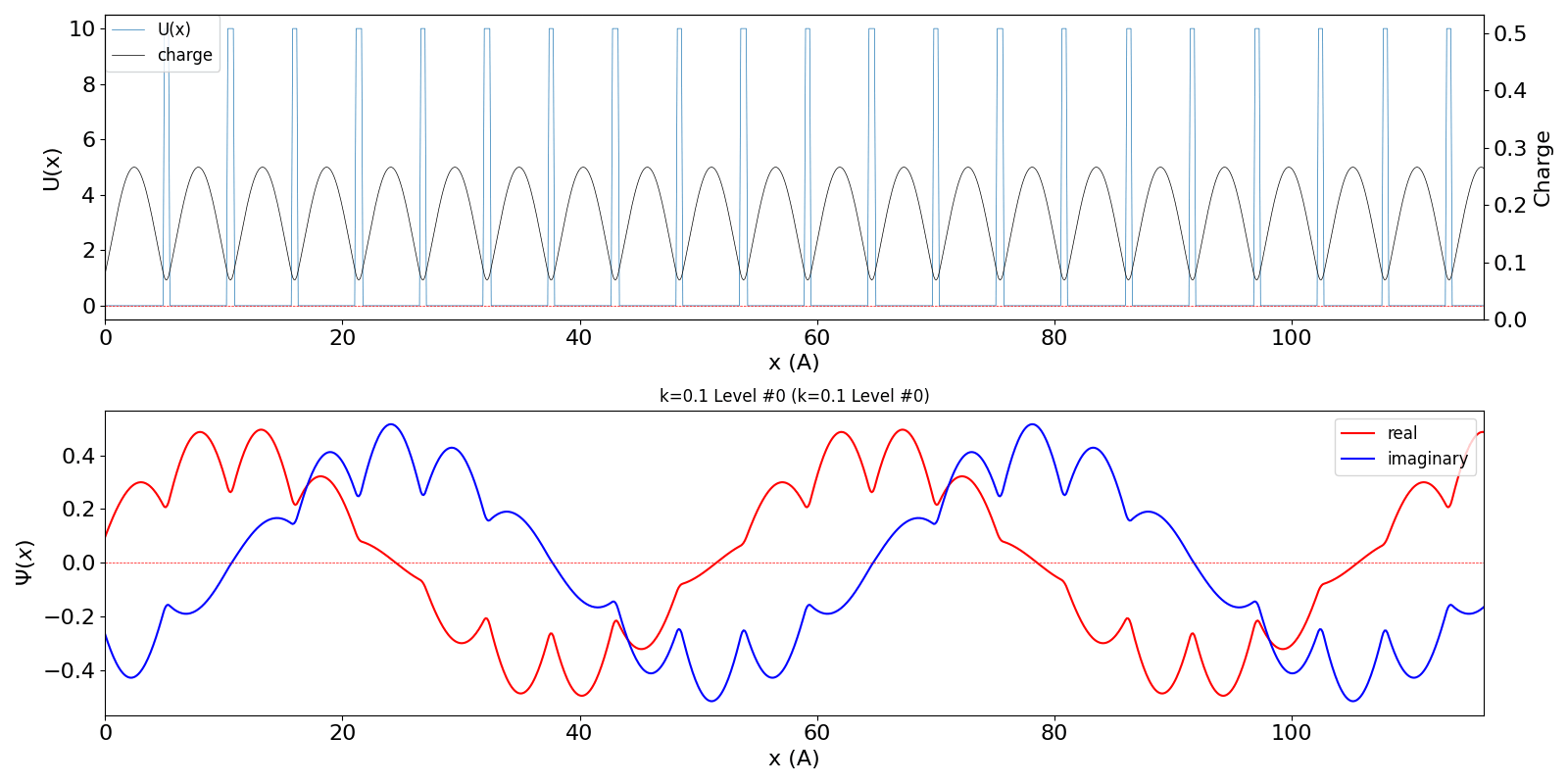
kronig_penney_wfanim_kw_0.1_Level_0.gif	kronig_penney_wfanim_kw_1.1_Level_0.gif	kronig_penney_wfanim_kw_0.1_Level_1.gif
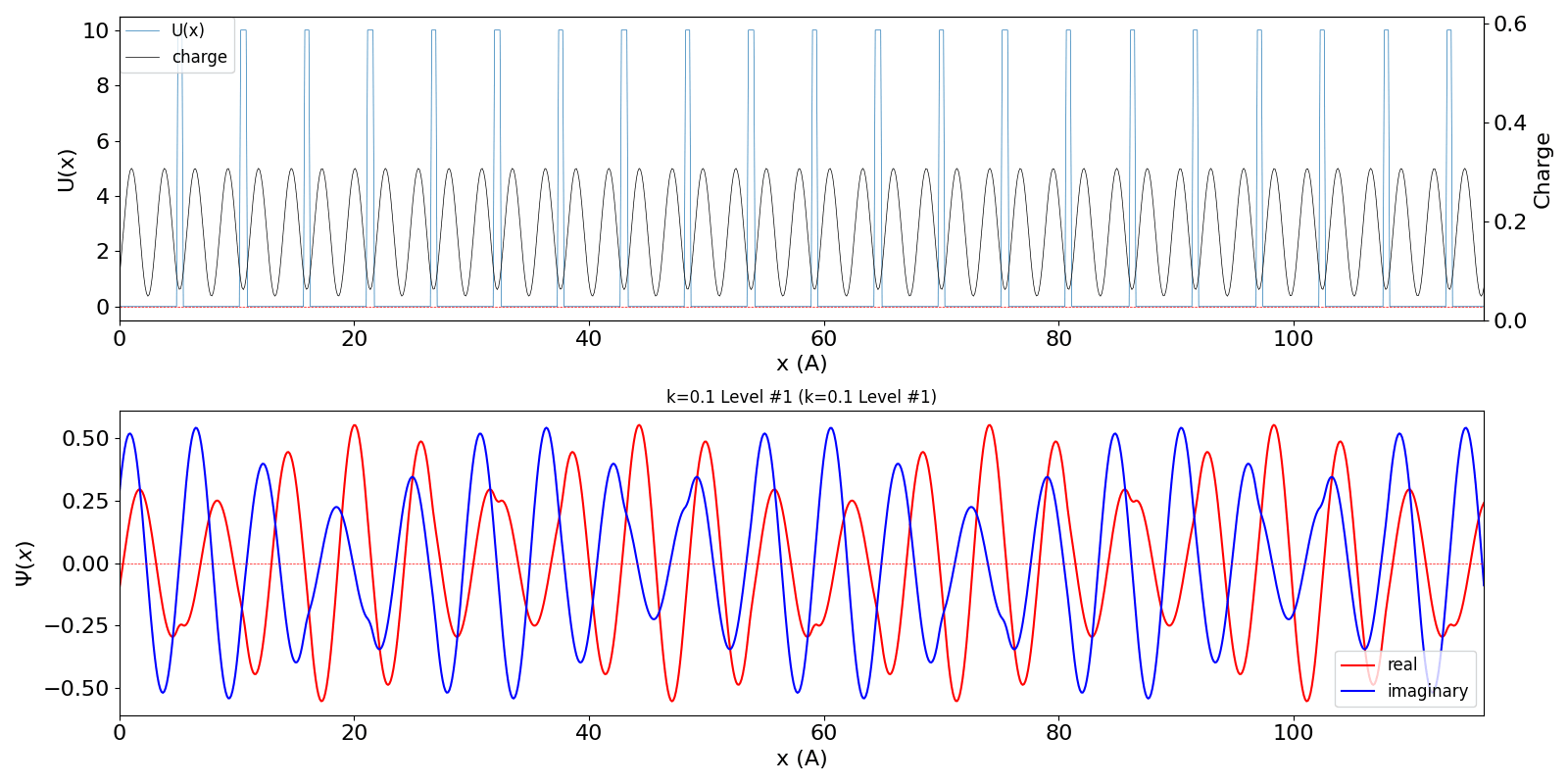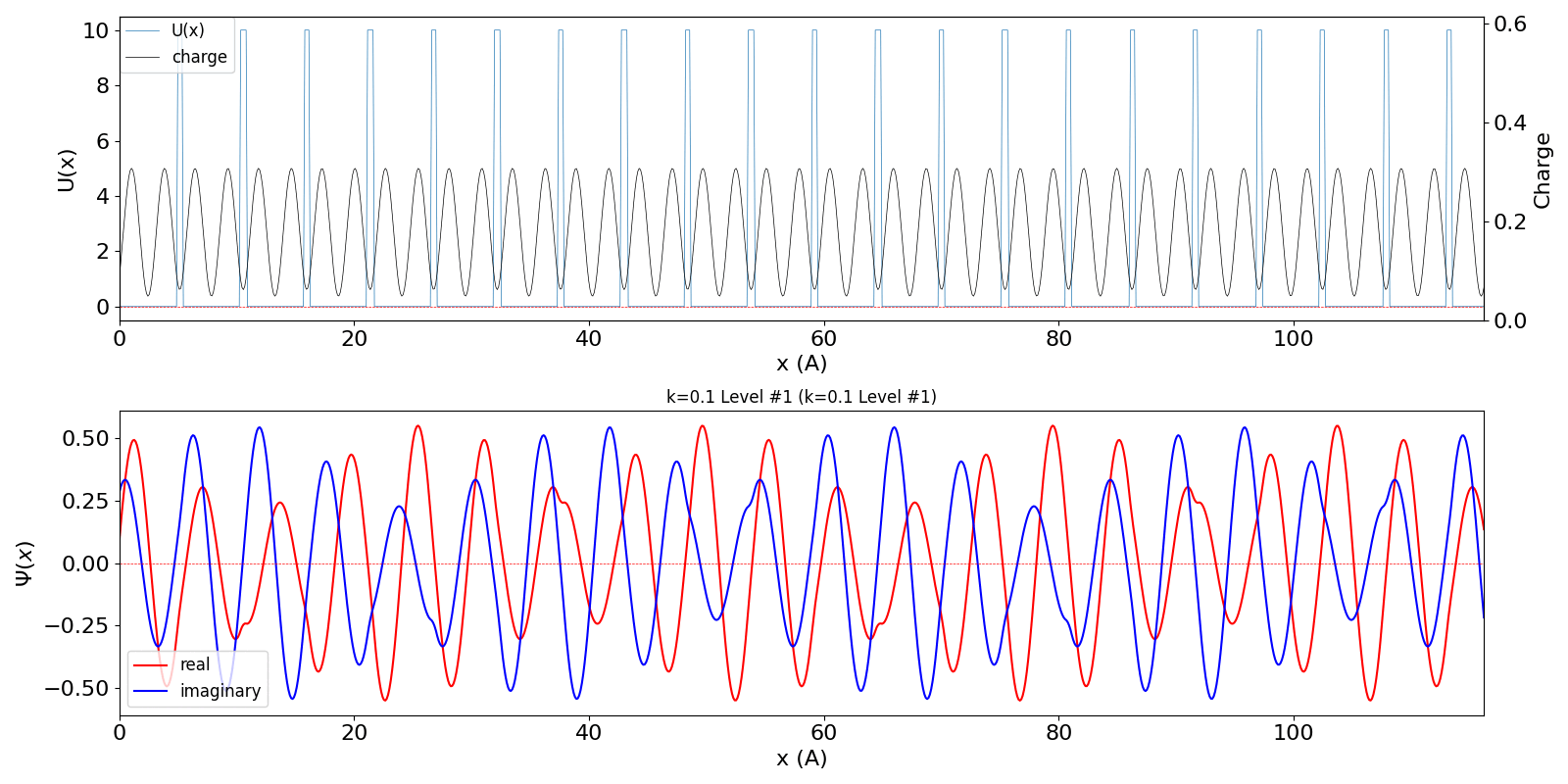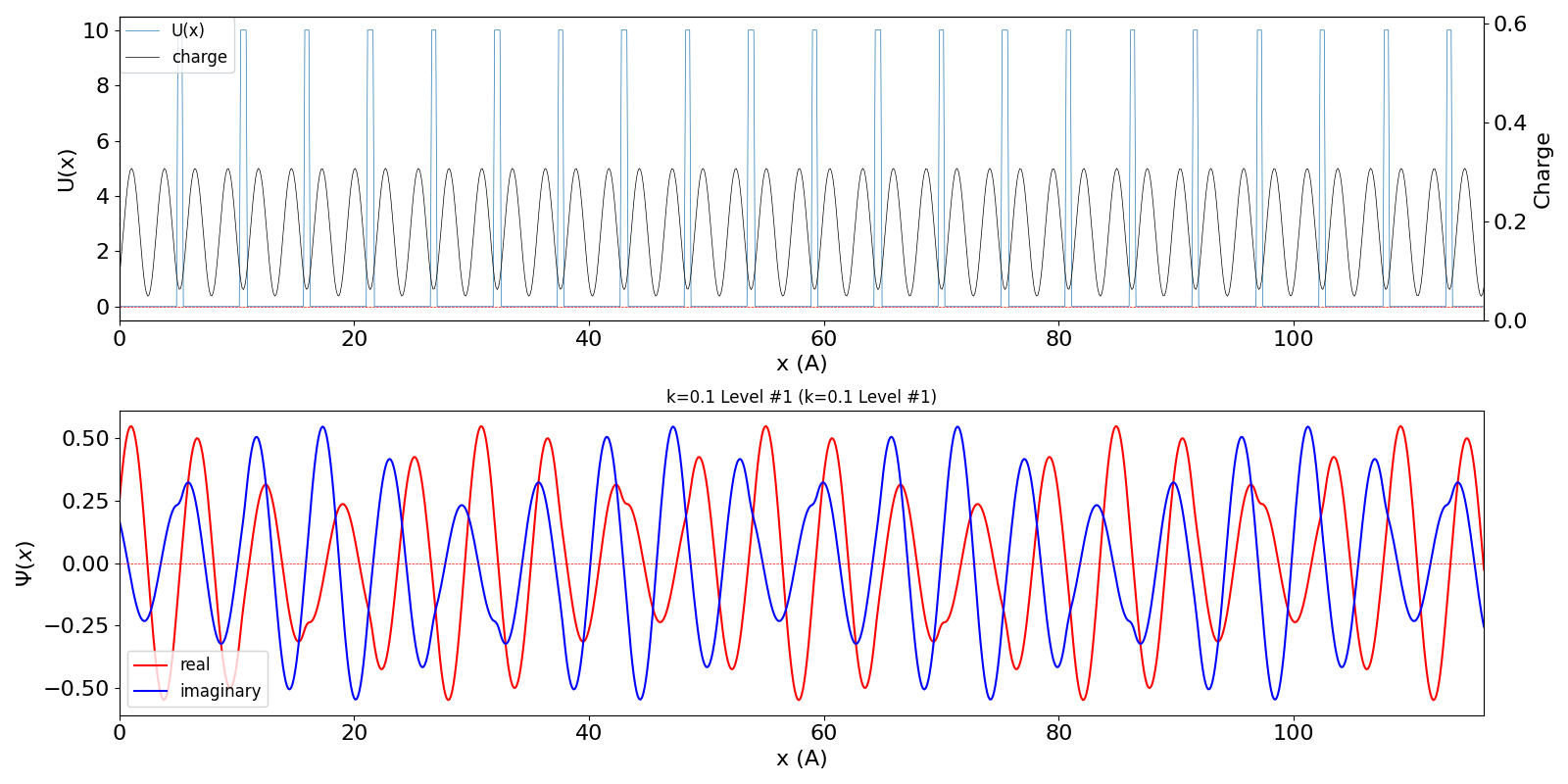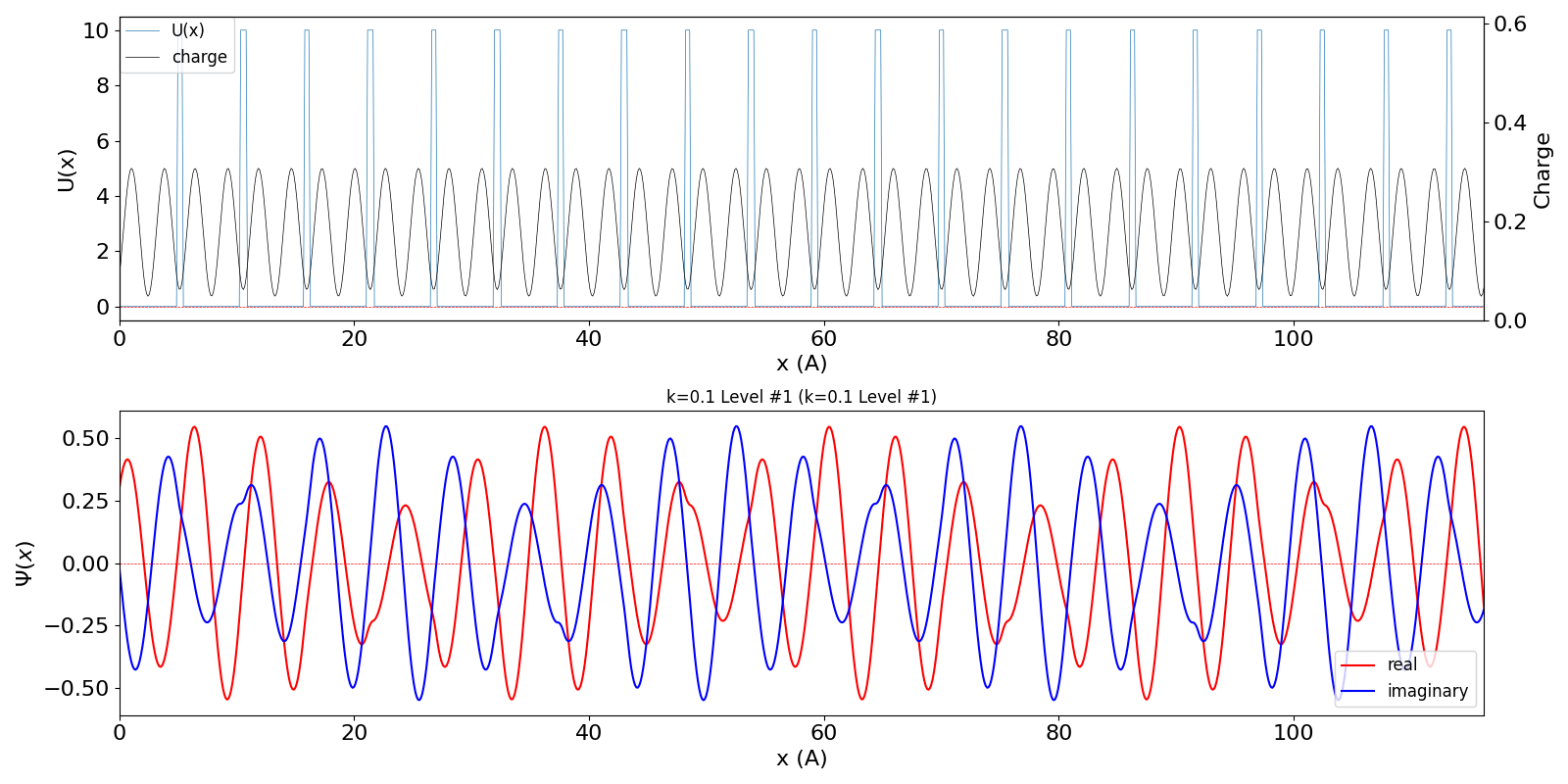
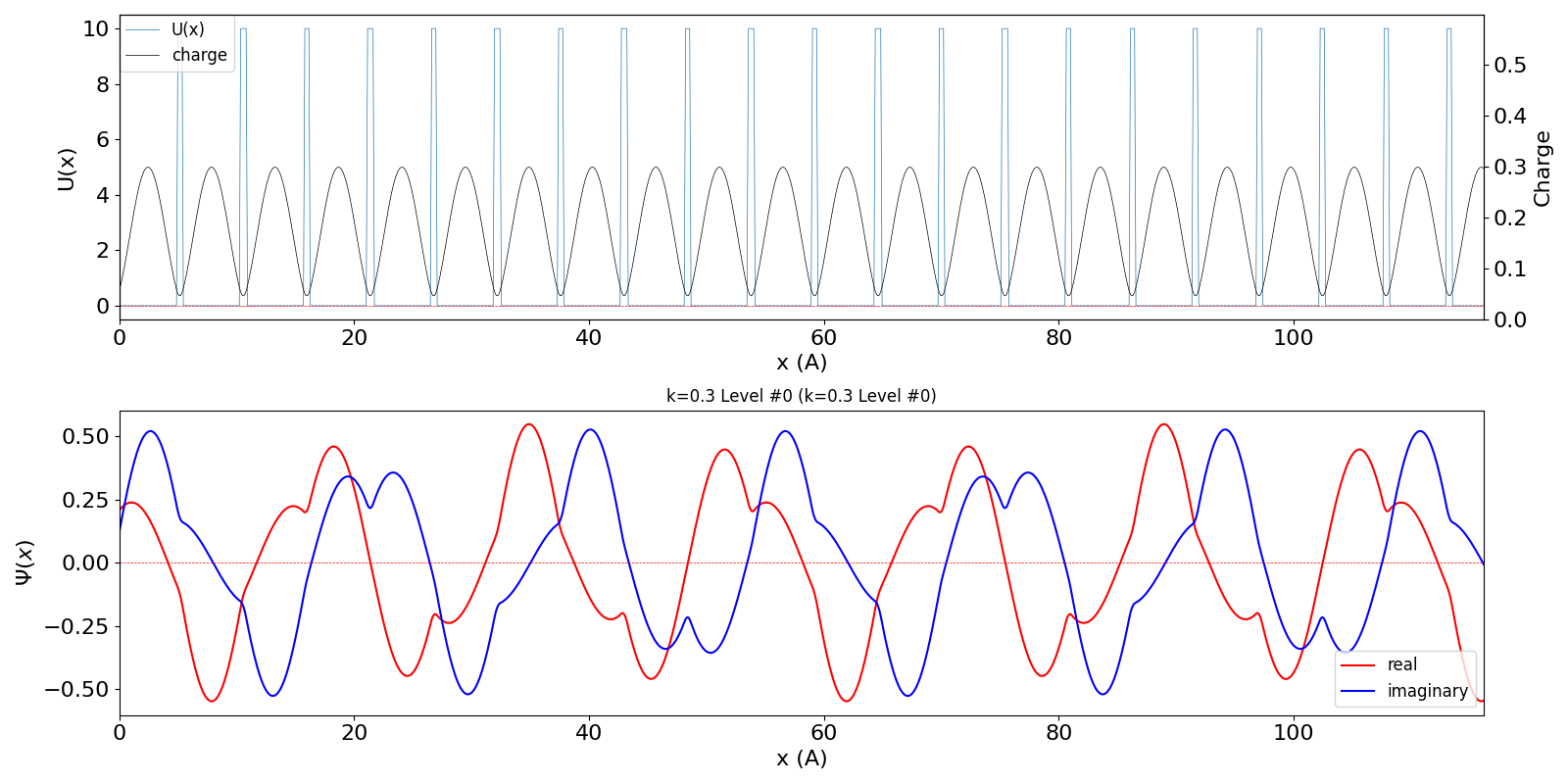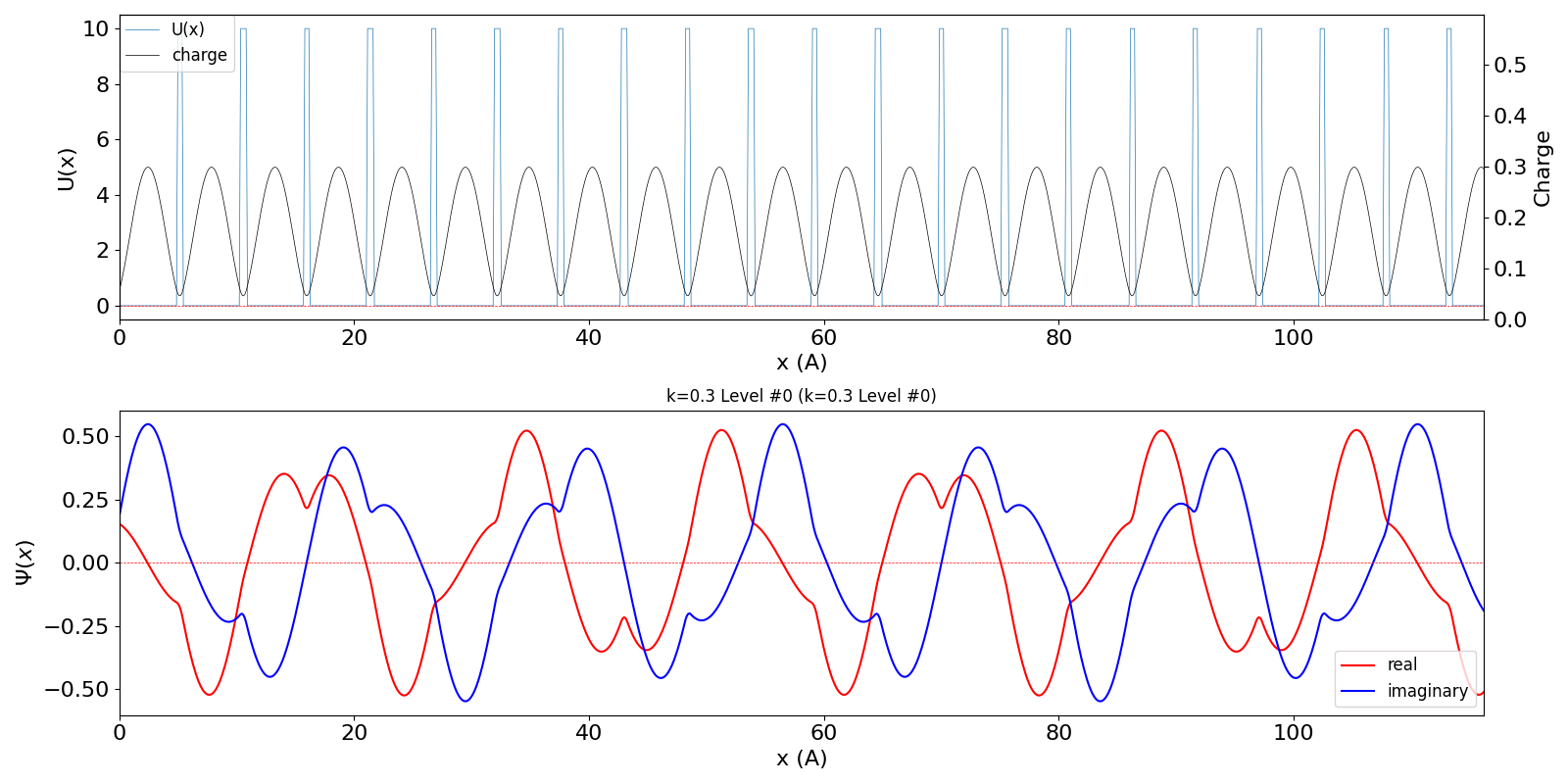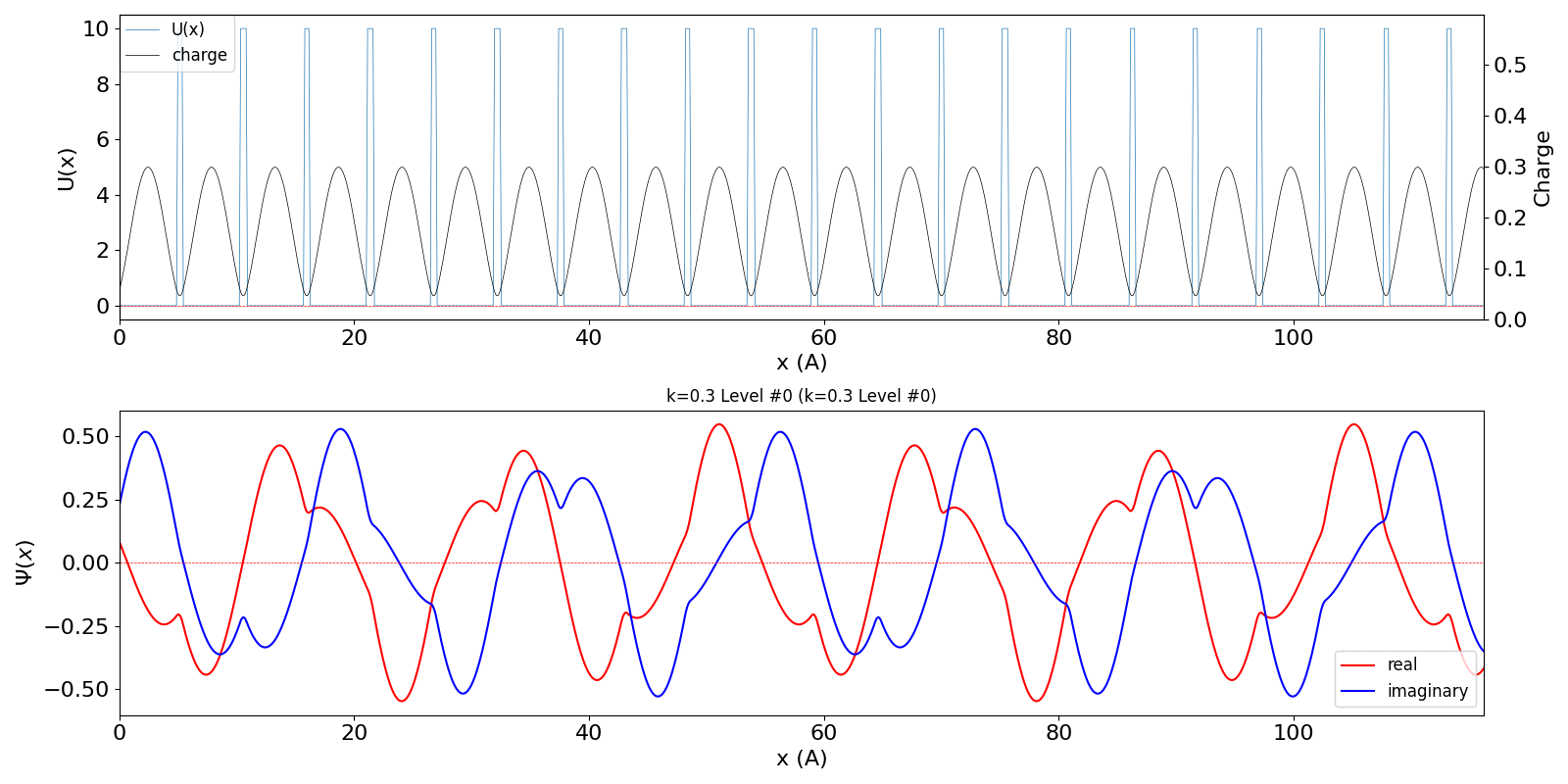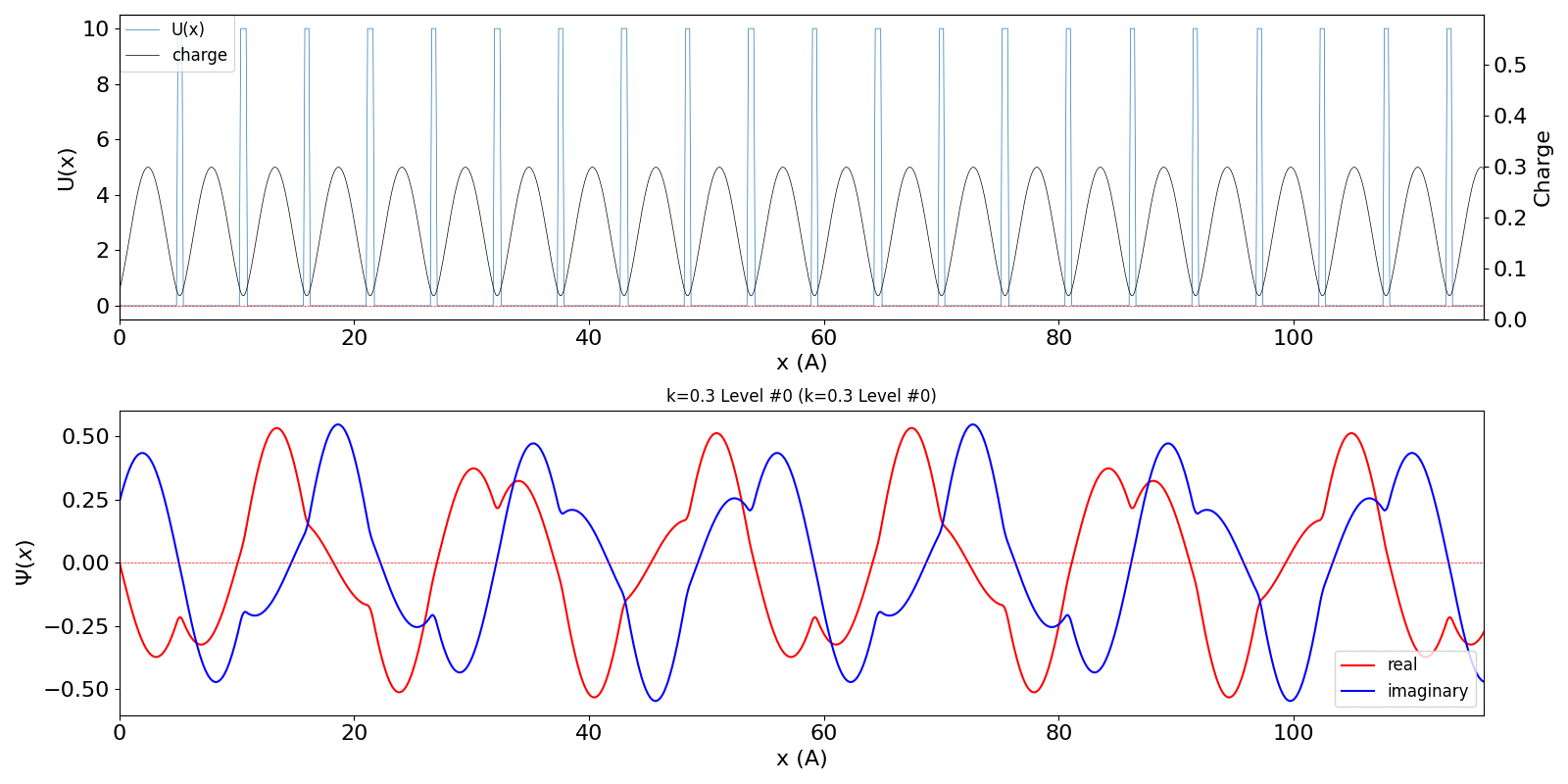
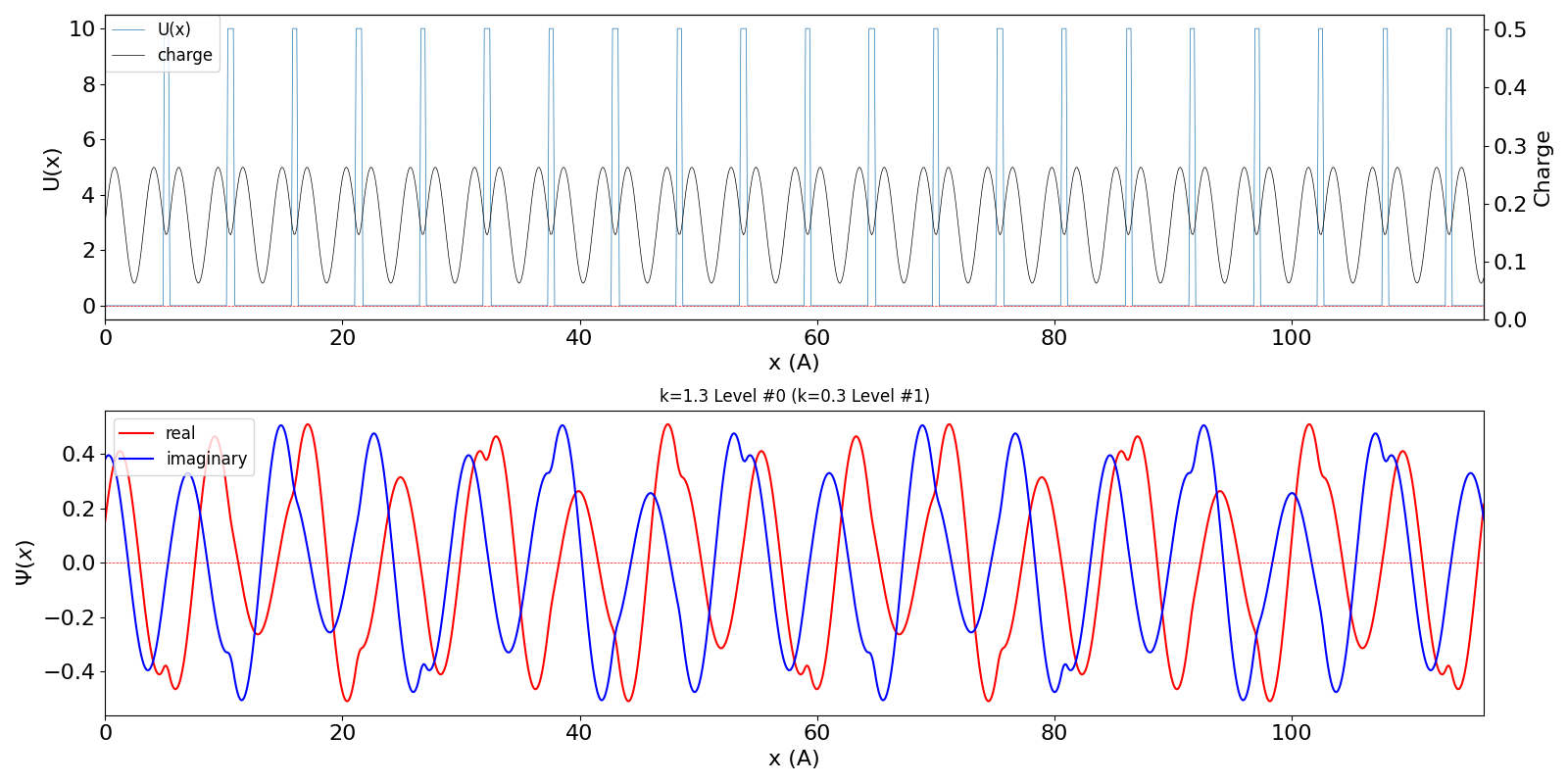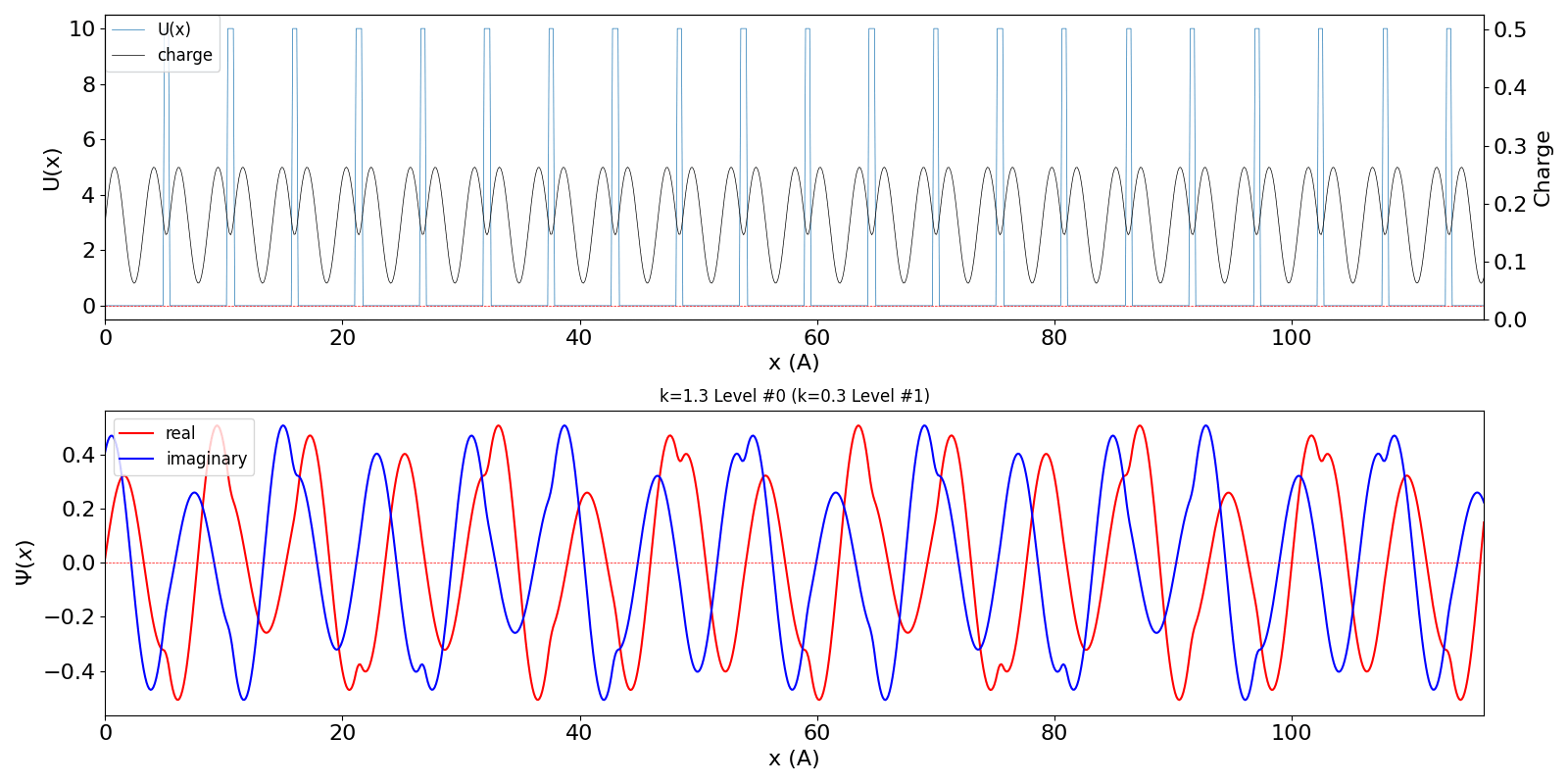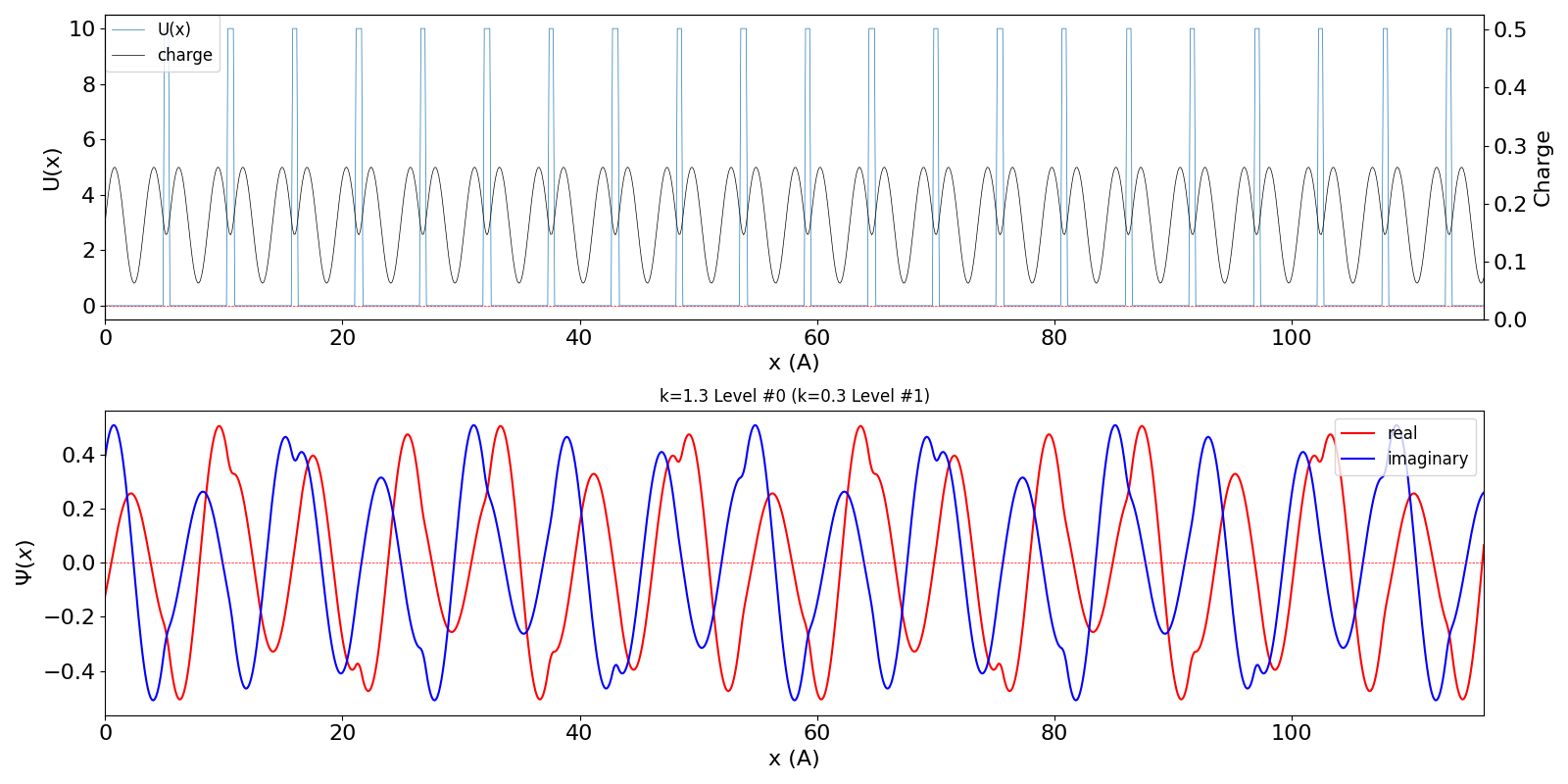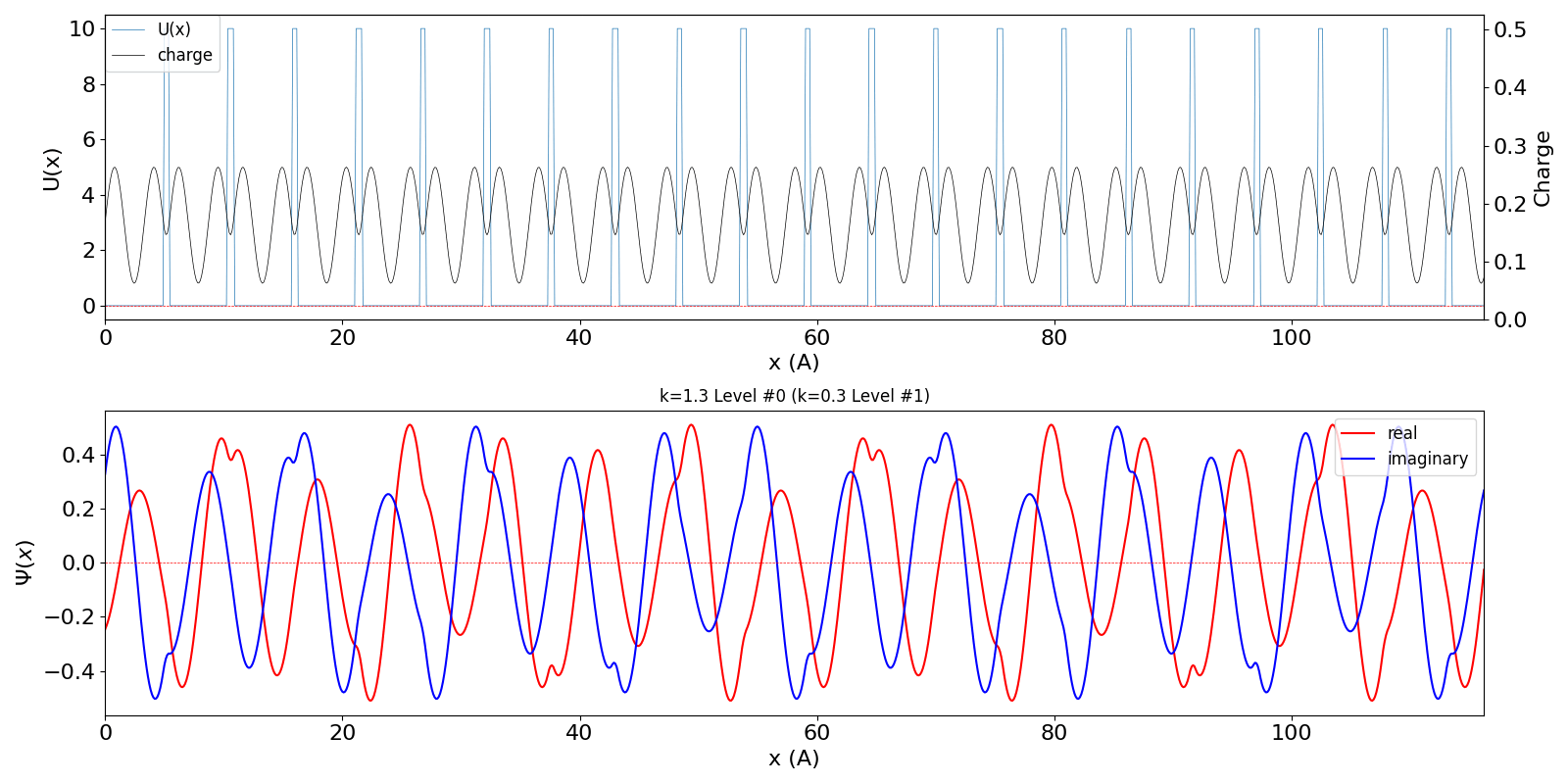
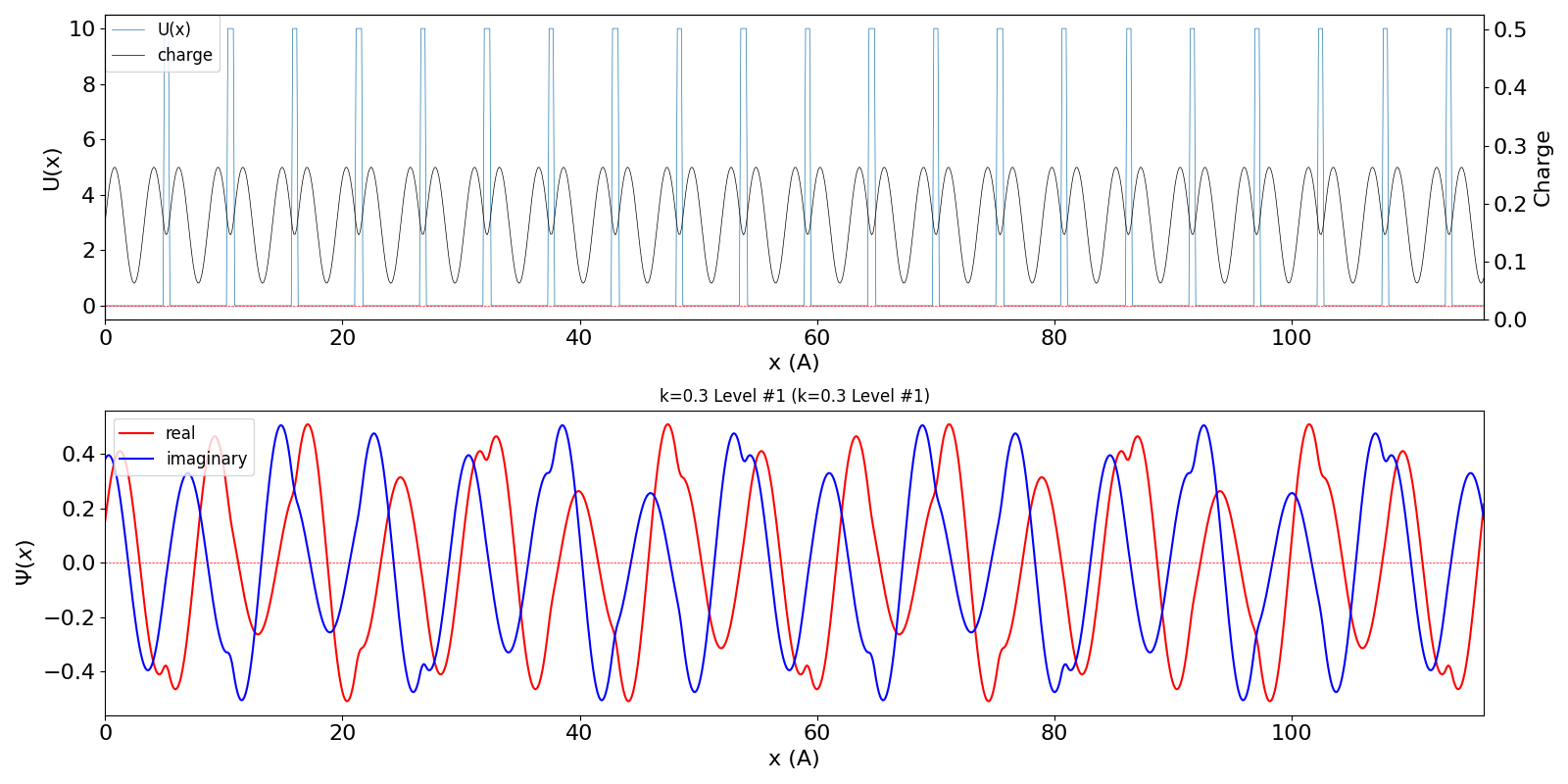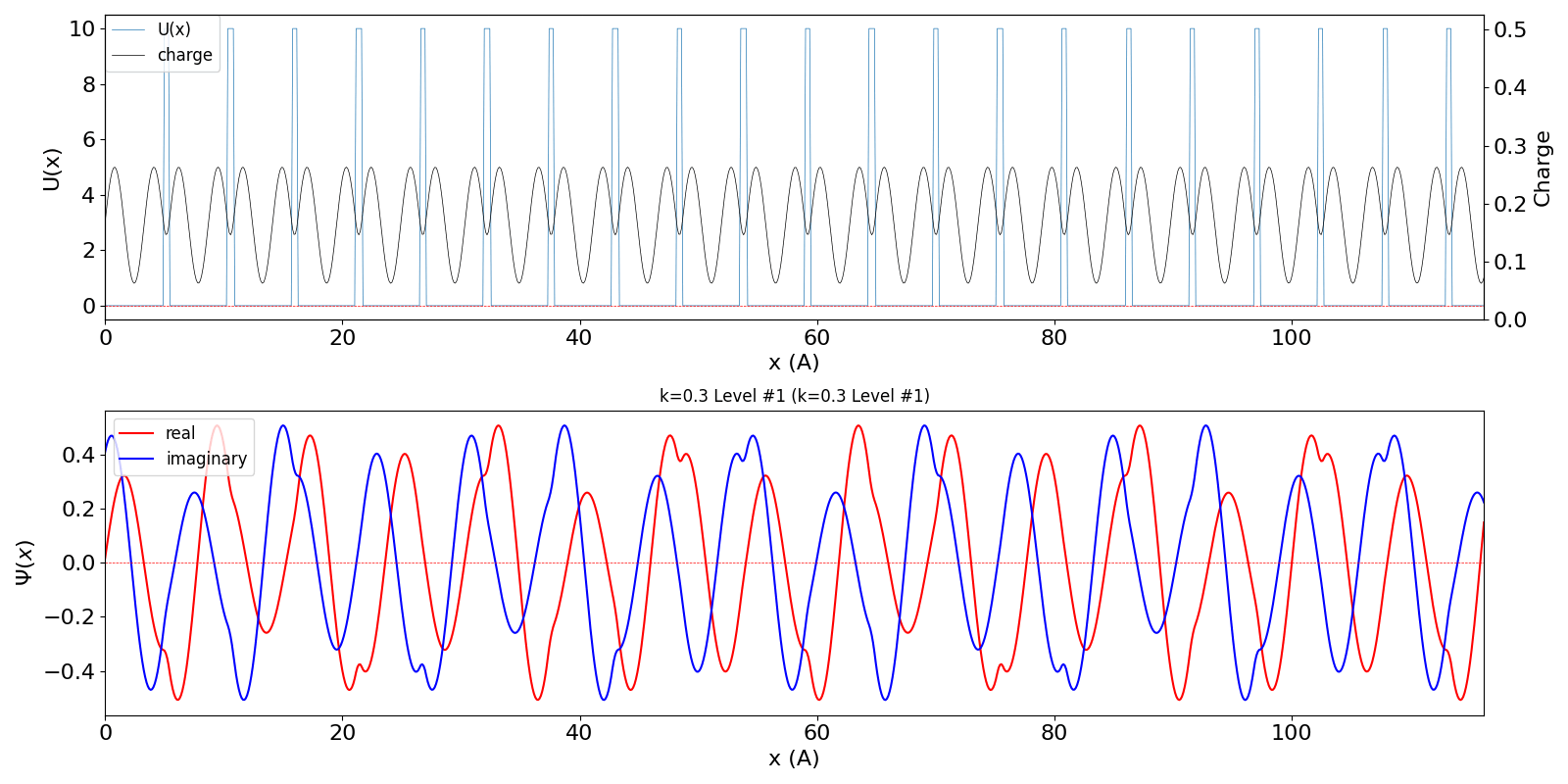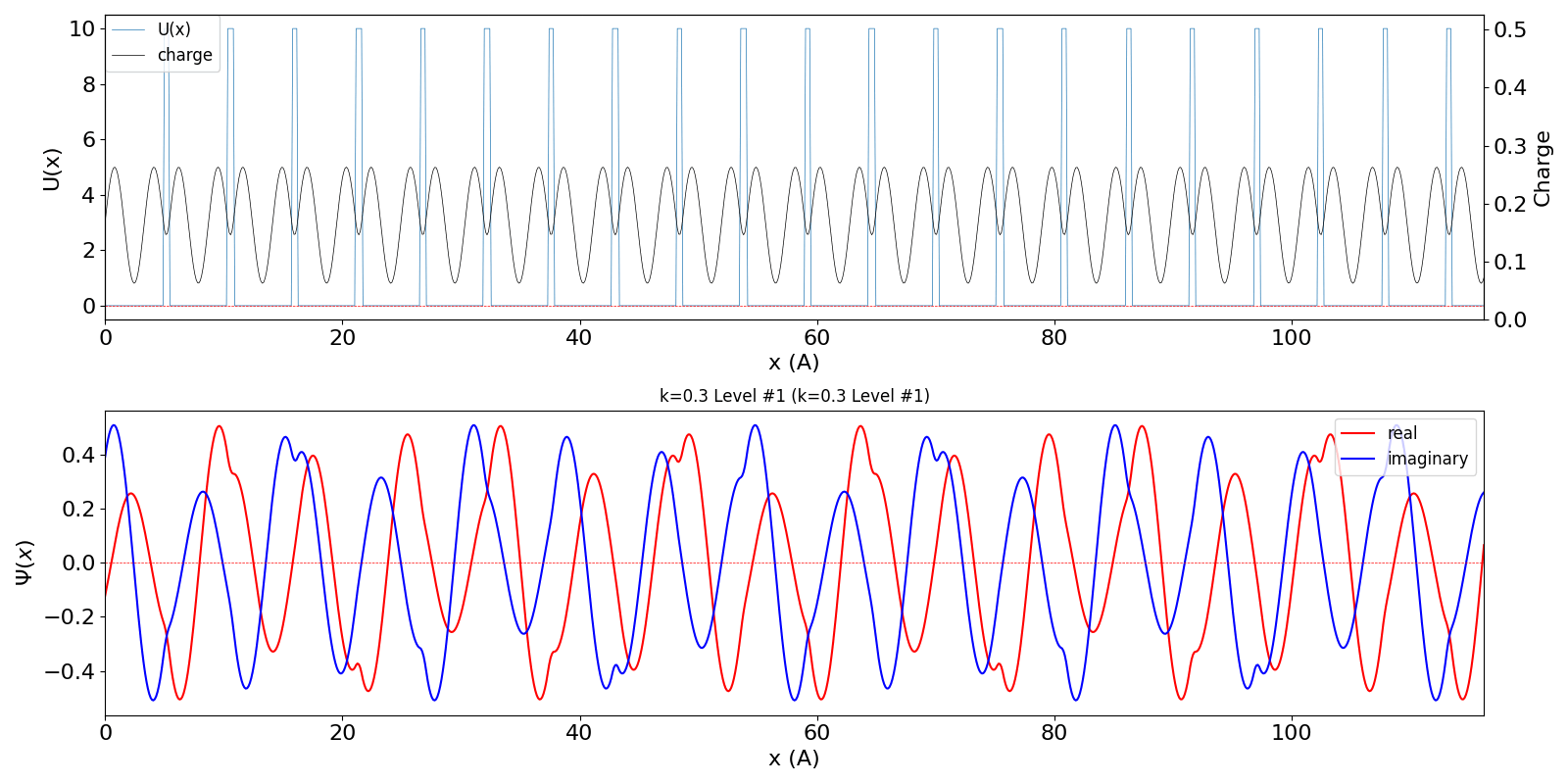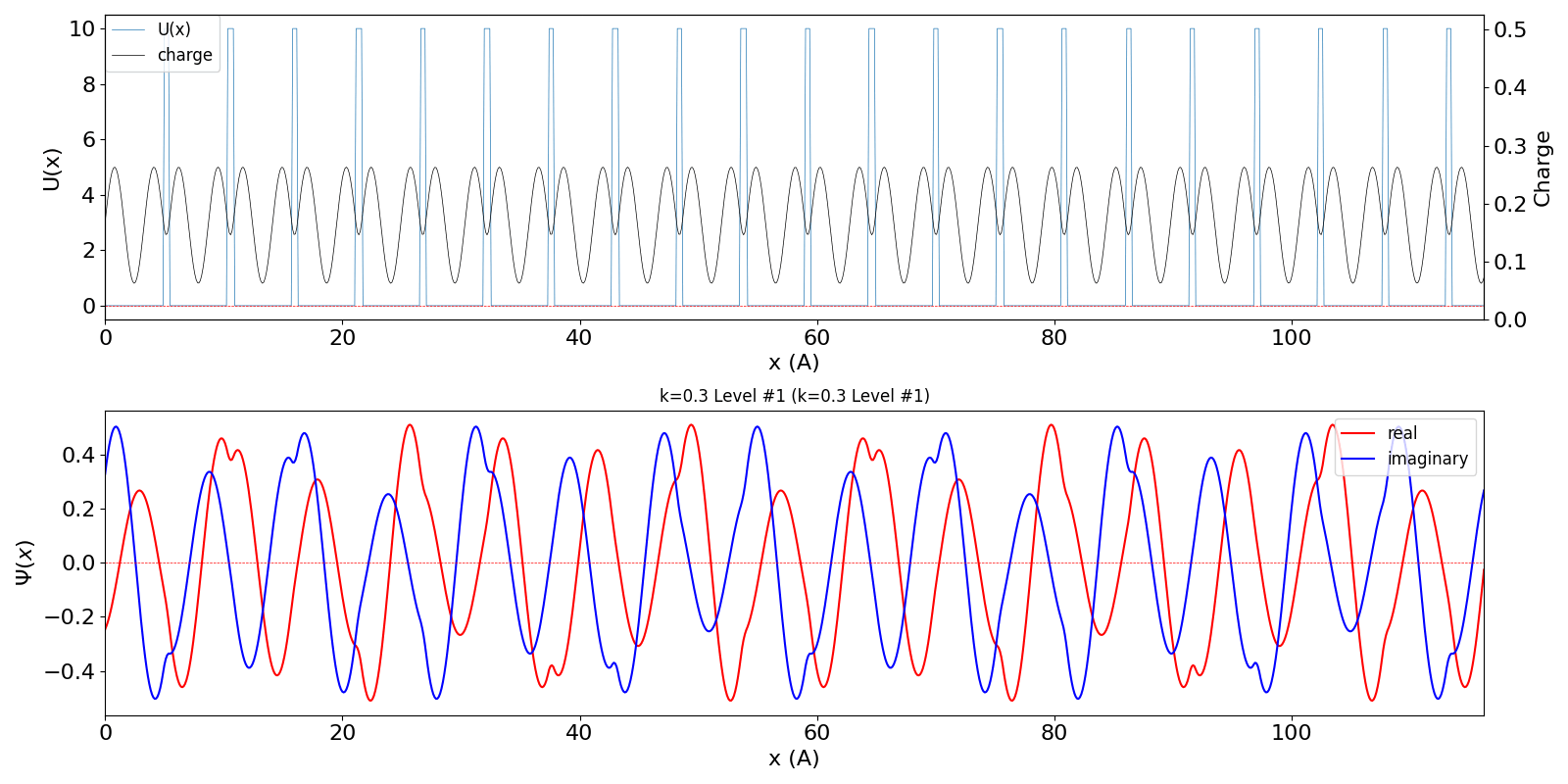
kw = 1.3 の波動関数 (中図) は、kw = 0.3 の第2準位 (右図) に対応しています。
kronig_penney_wfanim_kw_0.3_Level_0.gif	kronig_penney_wfanim_kw_1.3_Level_0.gif	kronig_penney_wfanim_kw_0.3_Level_1.gif
BZ境界 (kw = 0.5) の波動関数は、kw = 0.5 と kw = -0.5 (正確には、他に1.5, -1.5, ・・・など、周期性で等価な波数を全て含みますが、 教科書では２波近似をしています) が干渉するために定在波を作ります。 その結果、kw = 0.0と同様、包絡線は移動せず、電子の速度は 0 になります。 kw = 0.5 と kw = -0.5 の波動関数が干渉 (混成) する結果、結合軌道が iLevel = 0 (左図)、反結合軌道が iLevel = 1 (右図) のようになり、 バンドギャップが生じます。
kronig_penney_wfanim_kw_0.5_Level_0.gif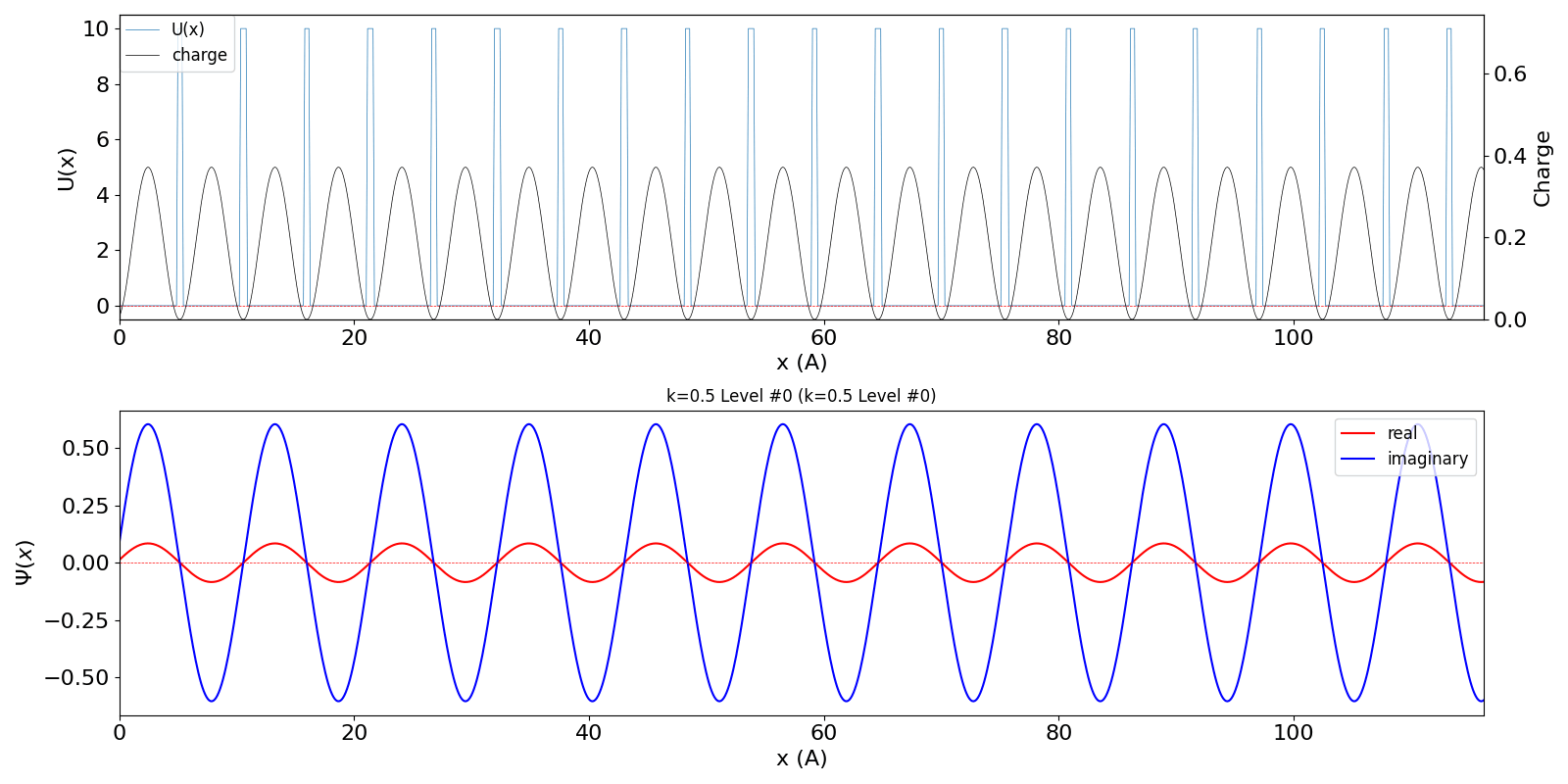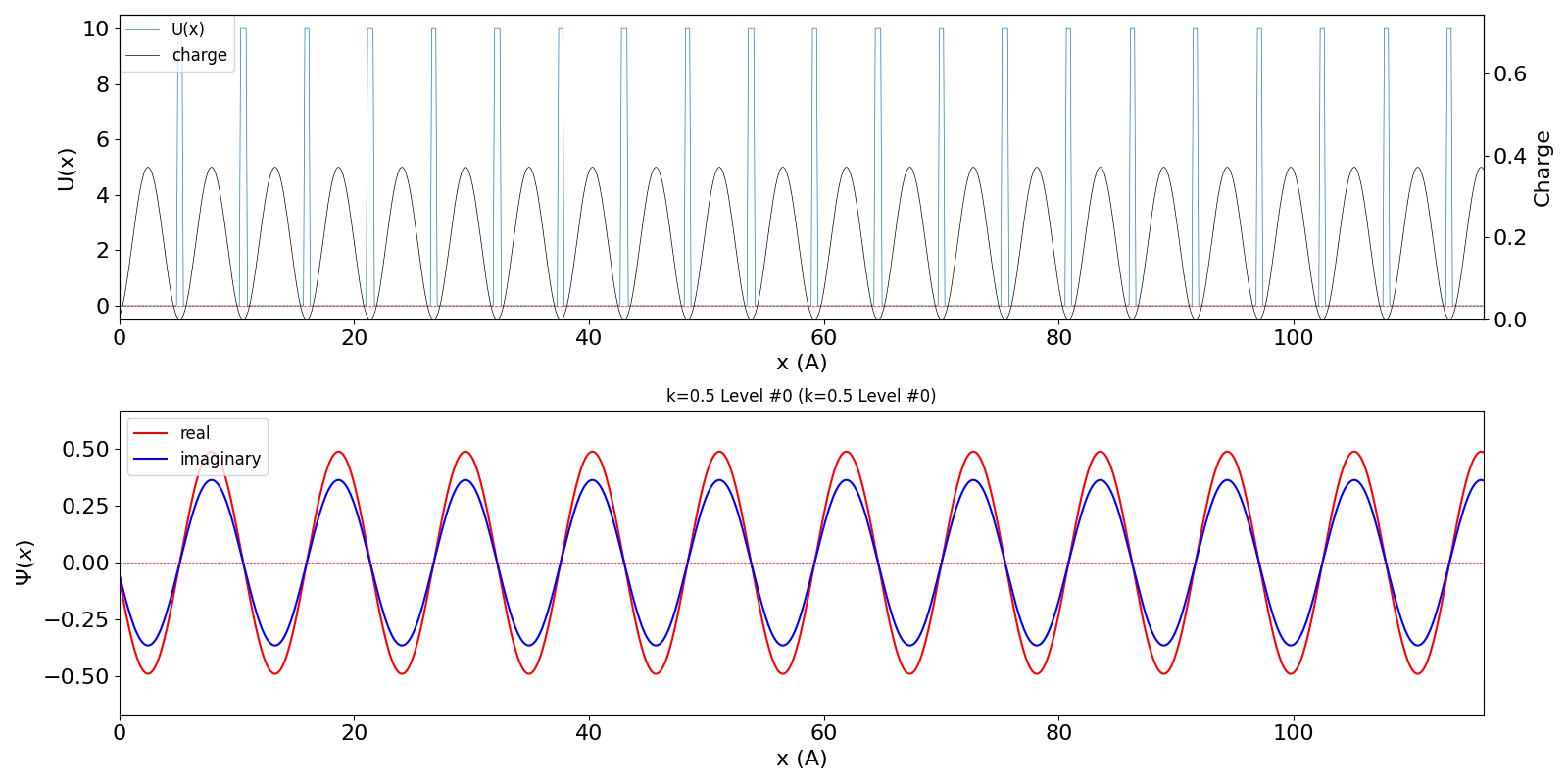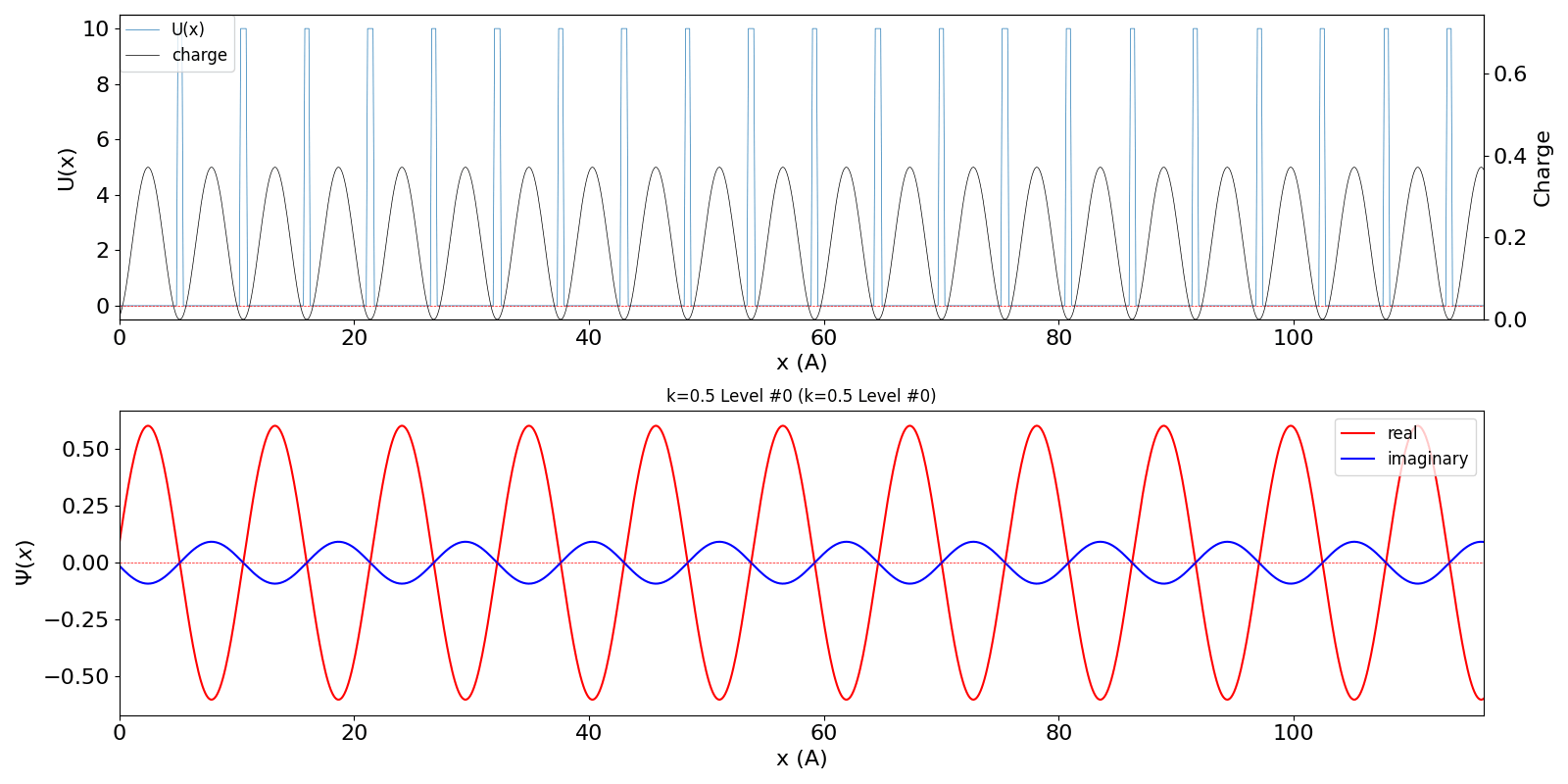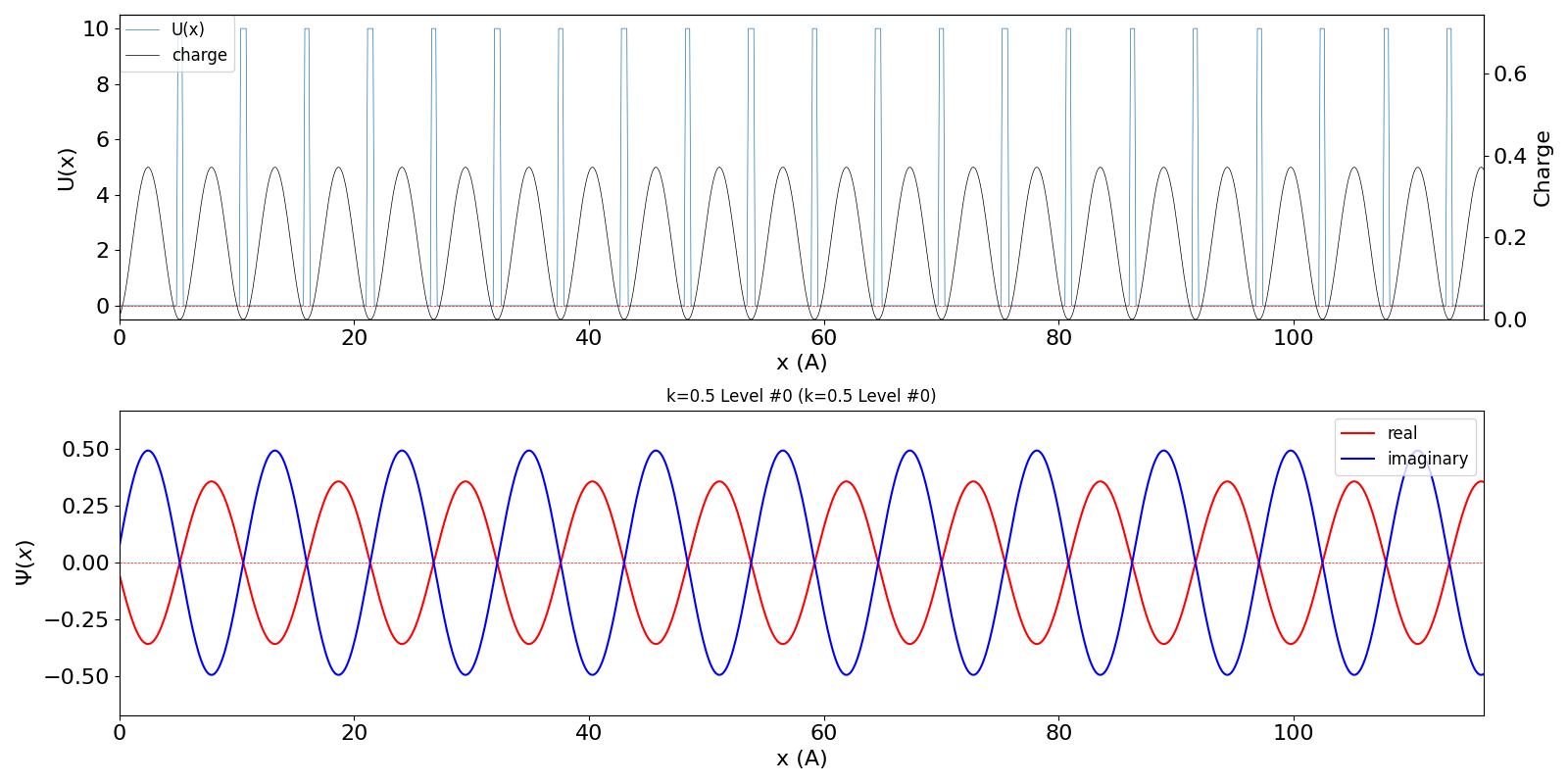	kronig_penney_wfanim_kw_0.5_Level_1.gif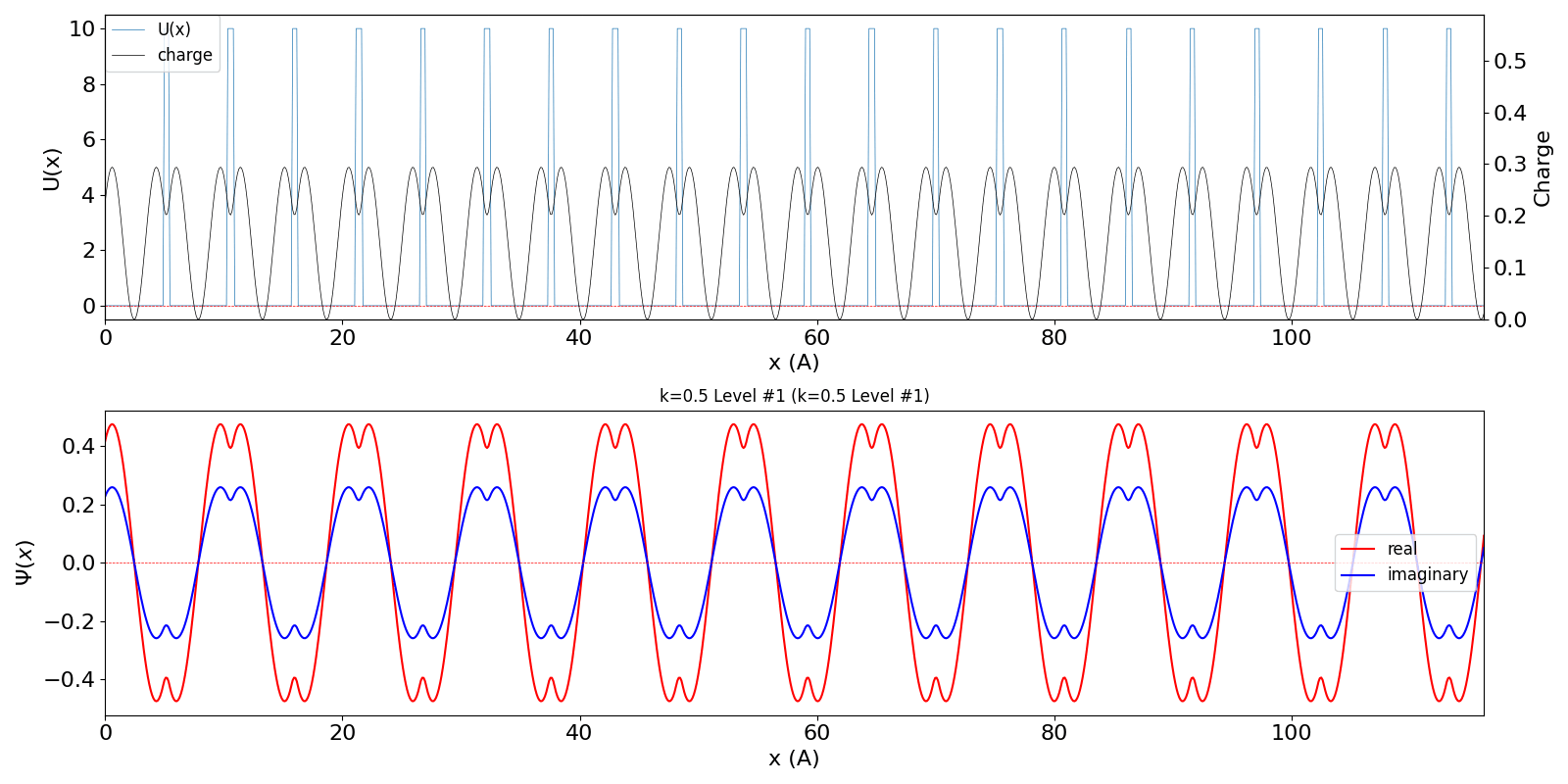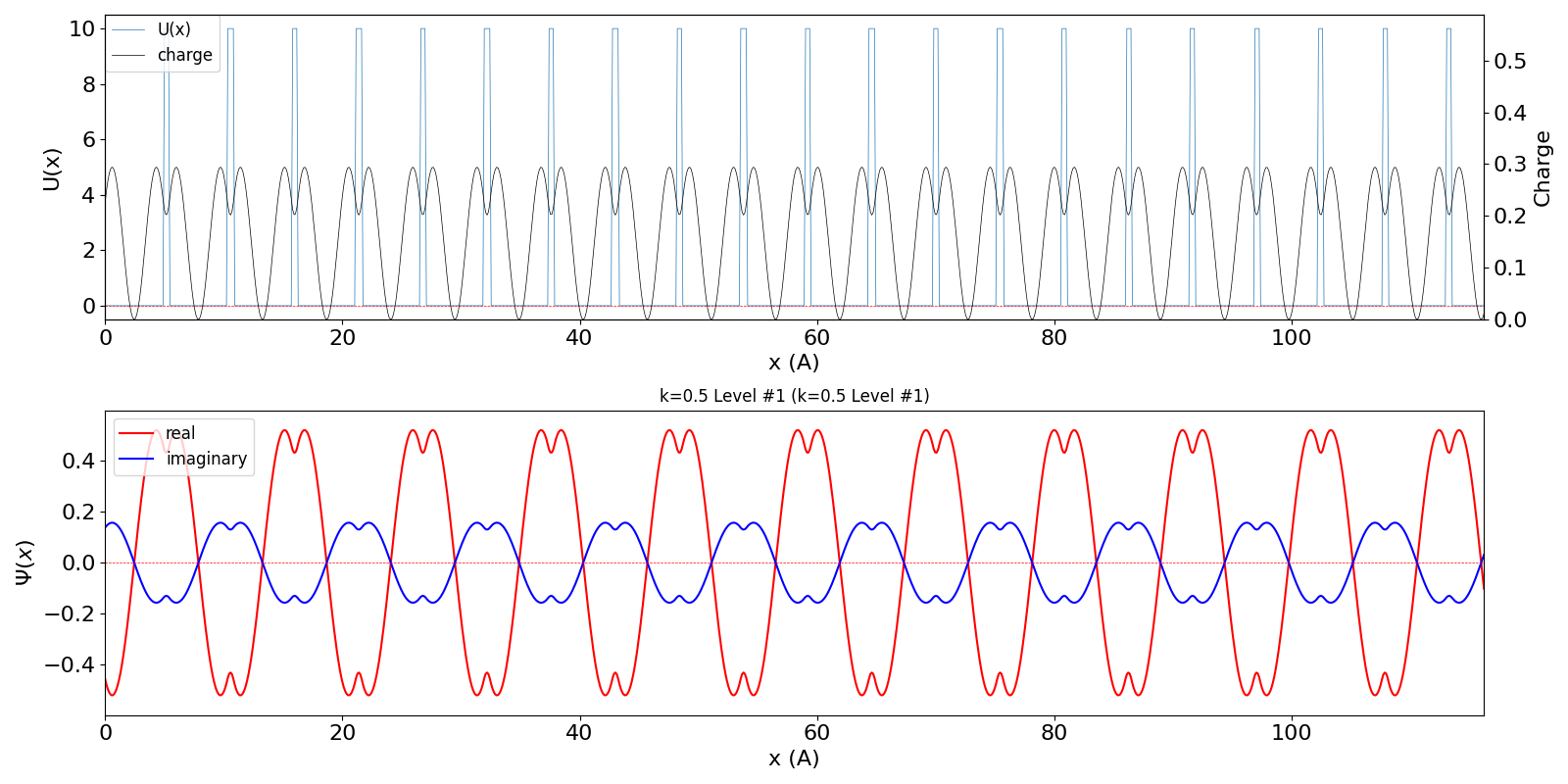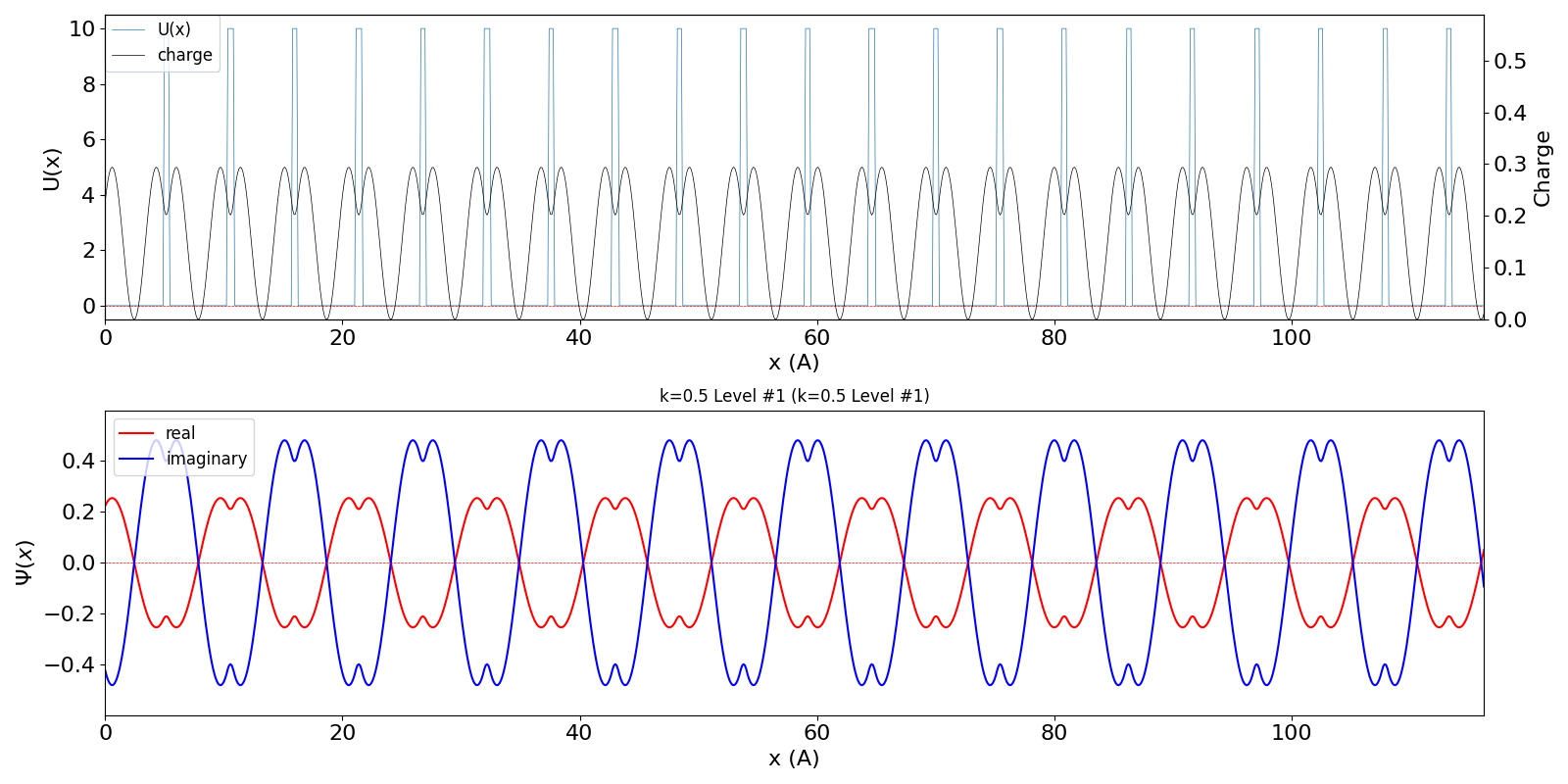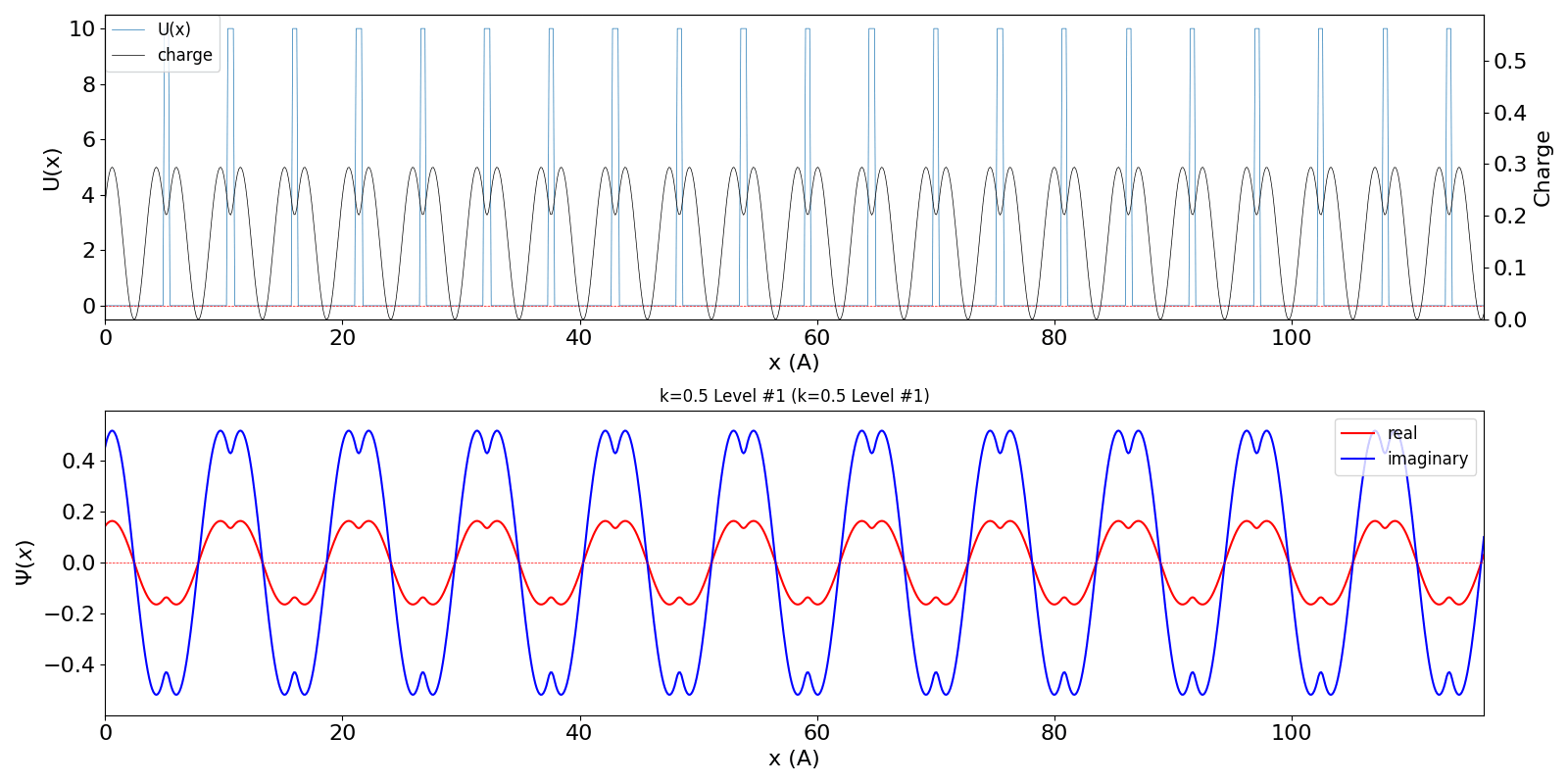
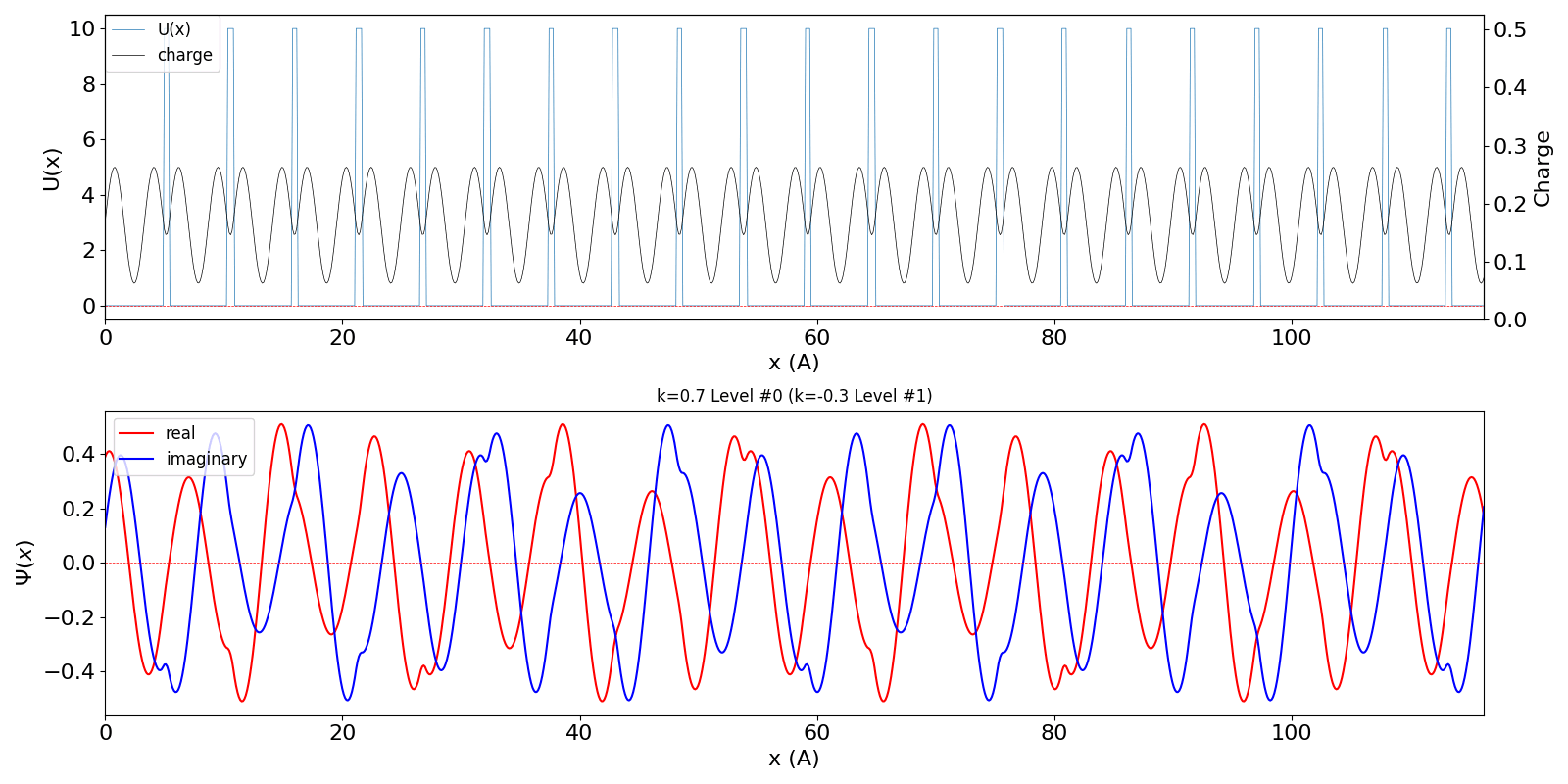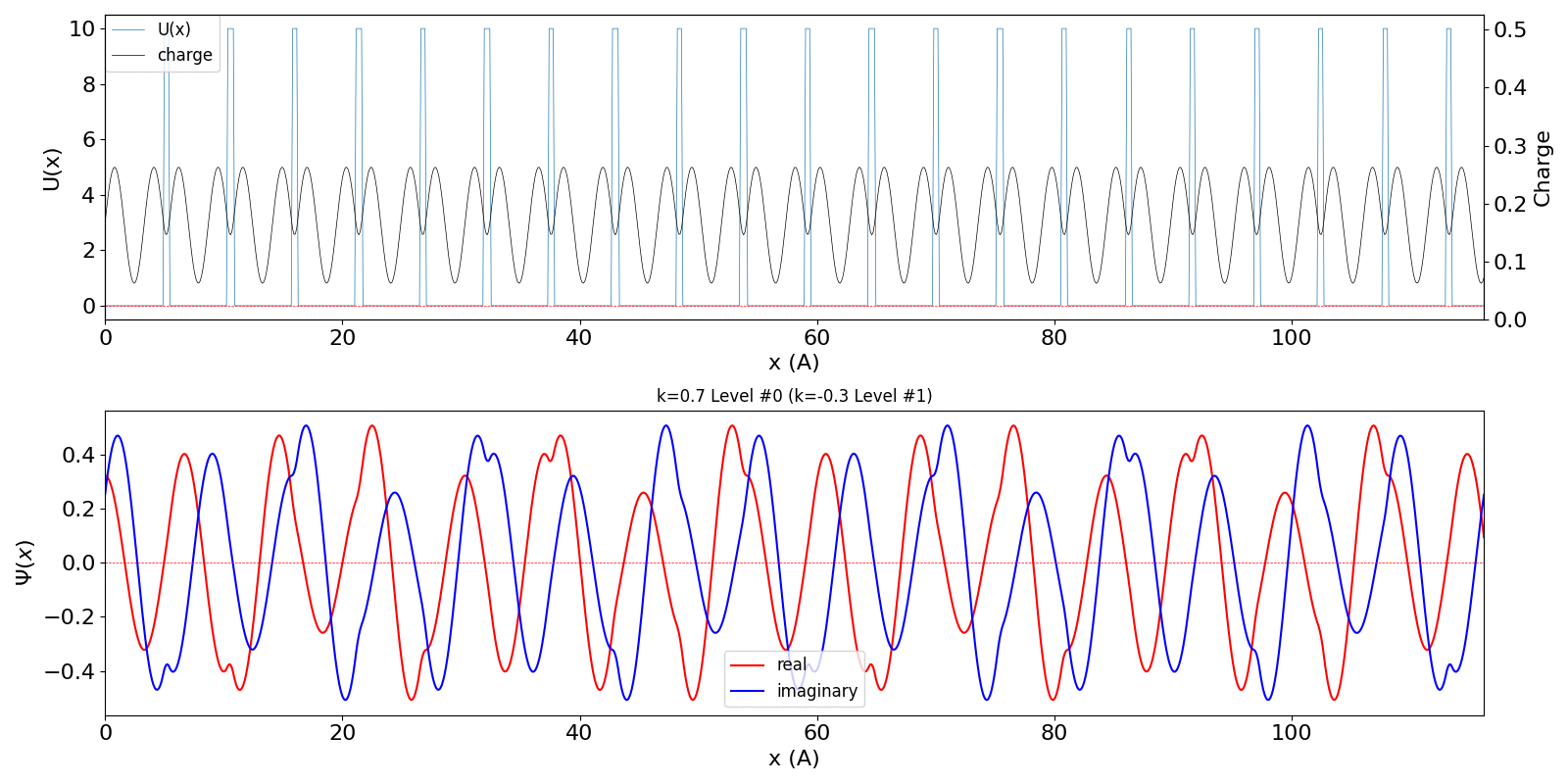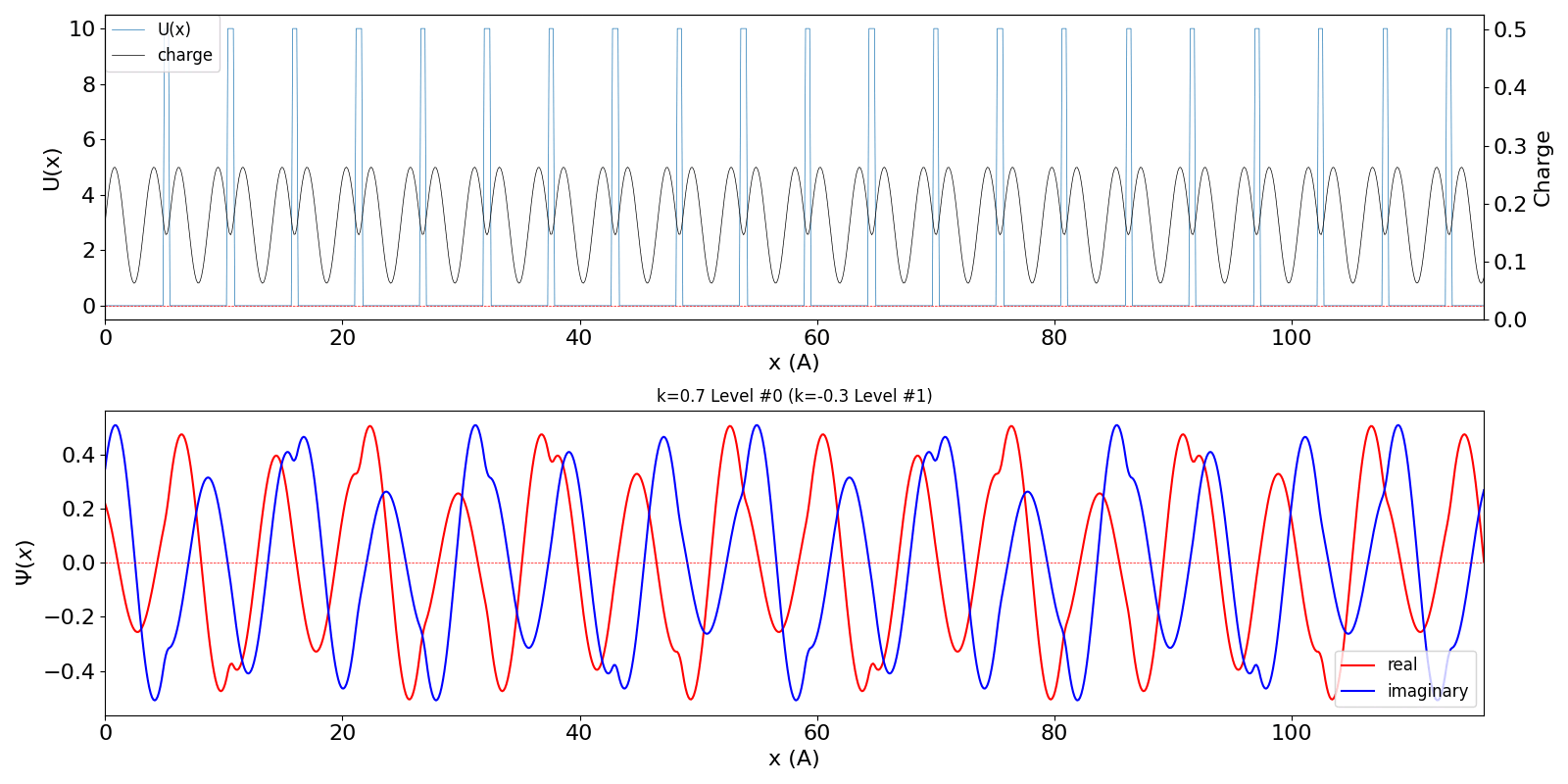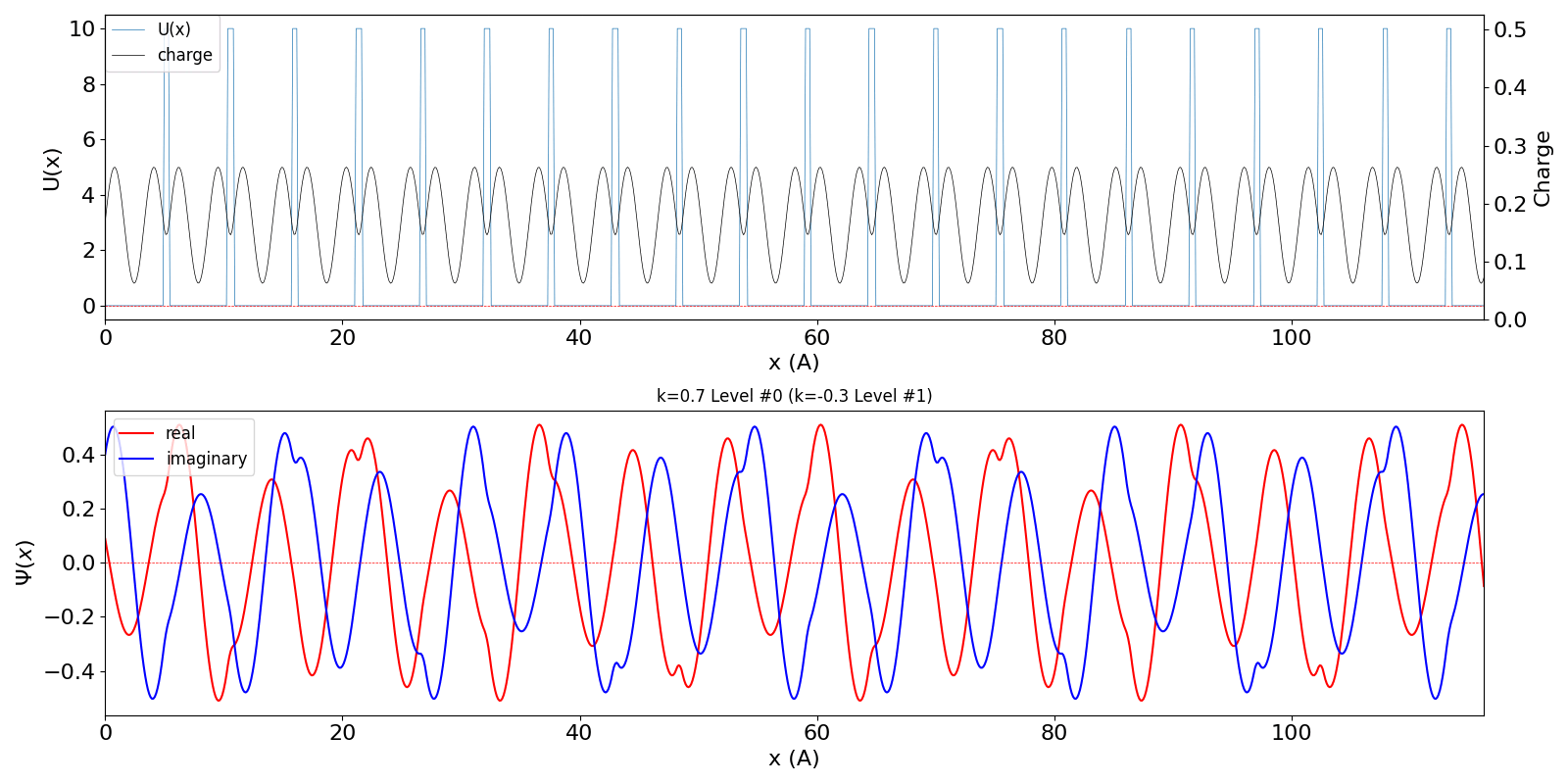
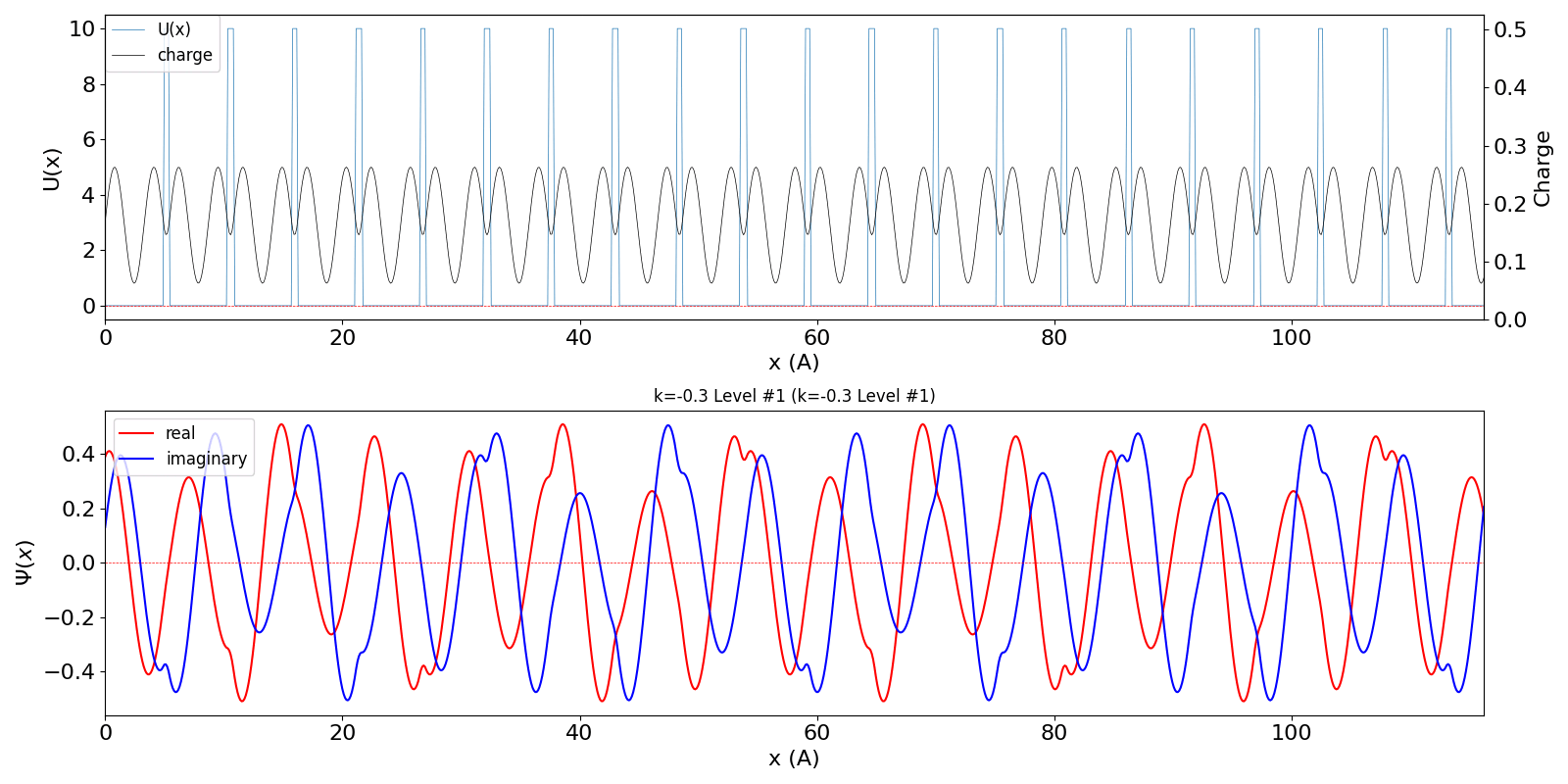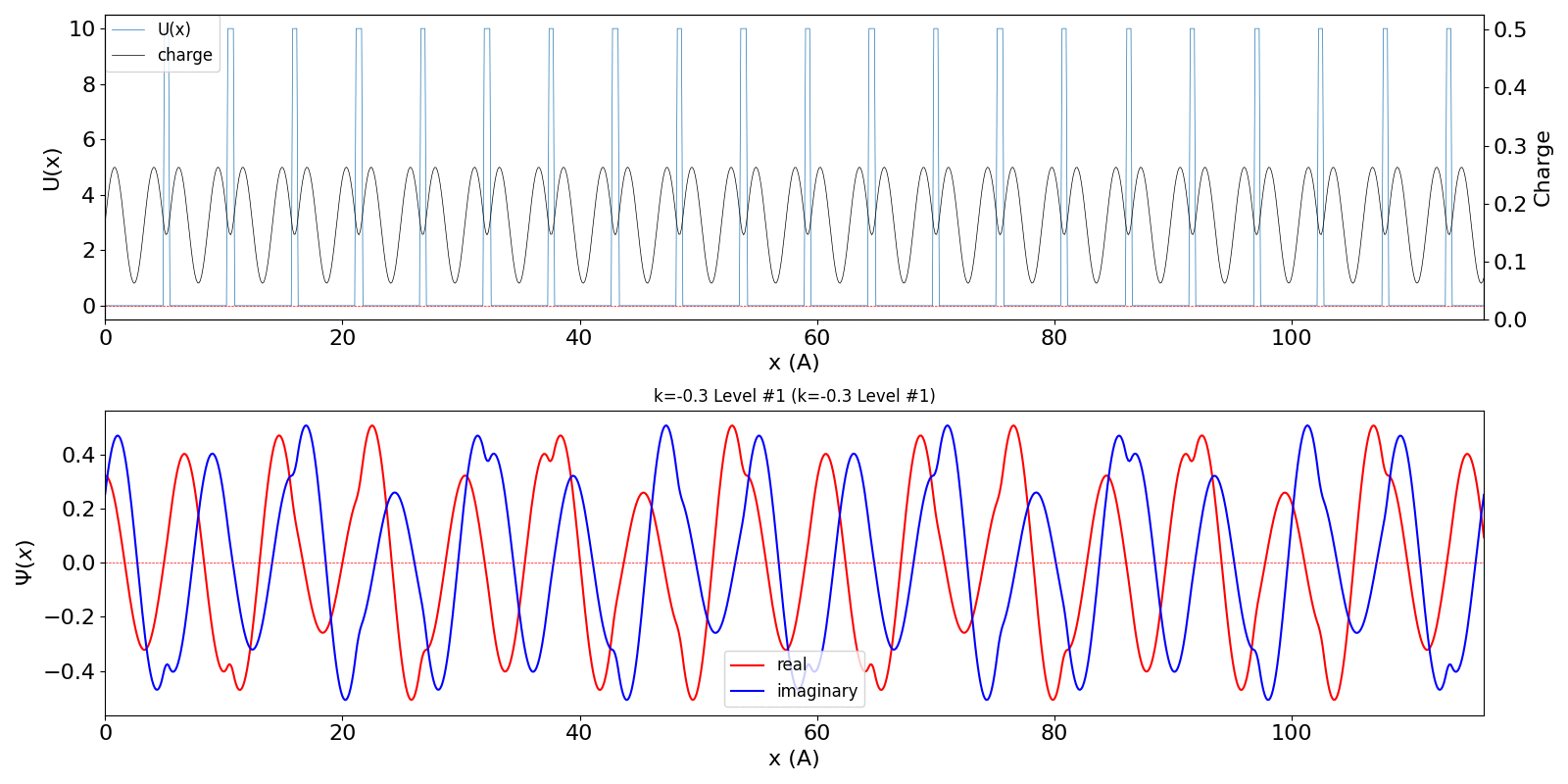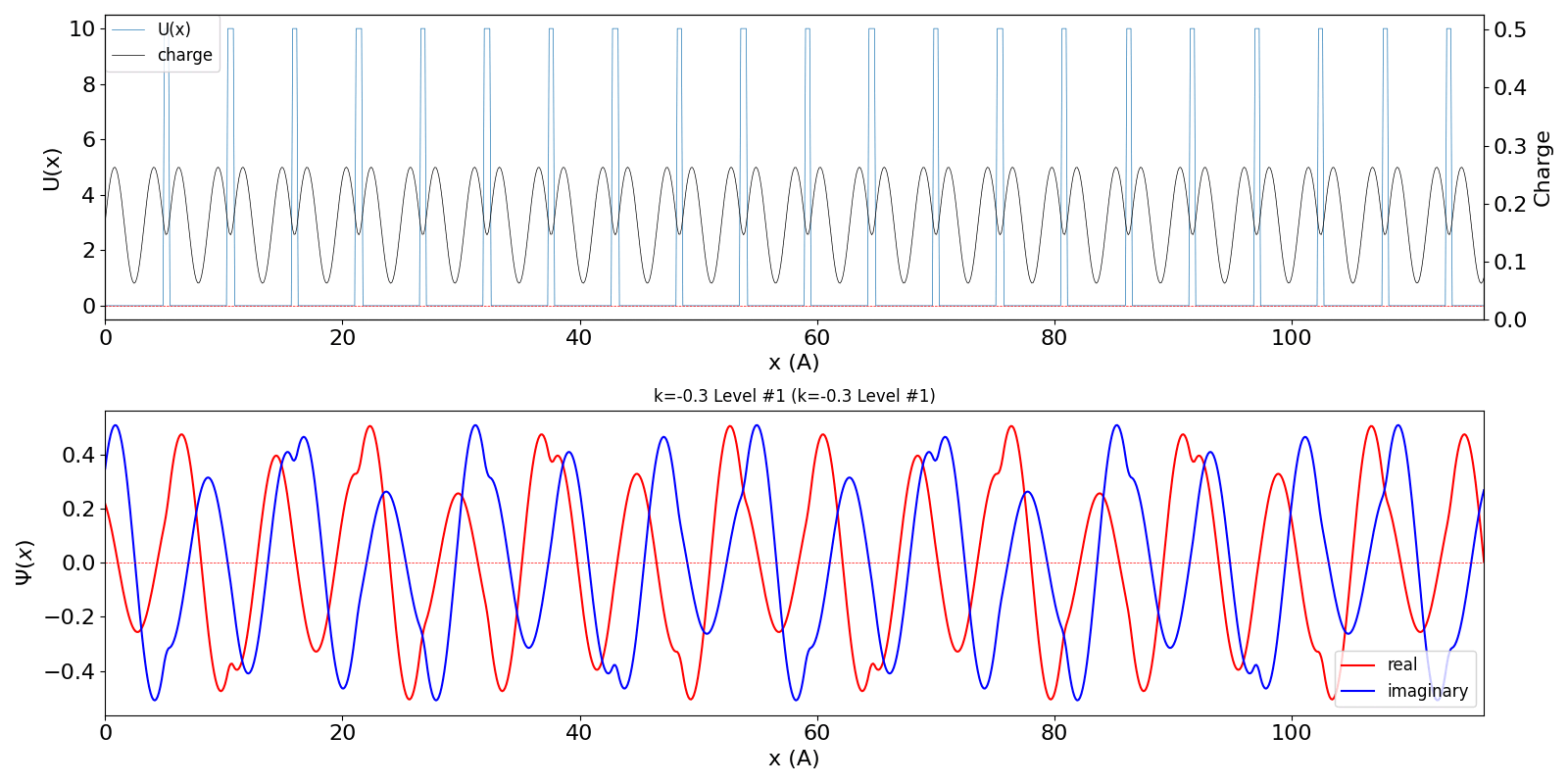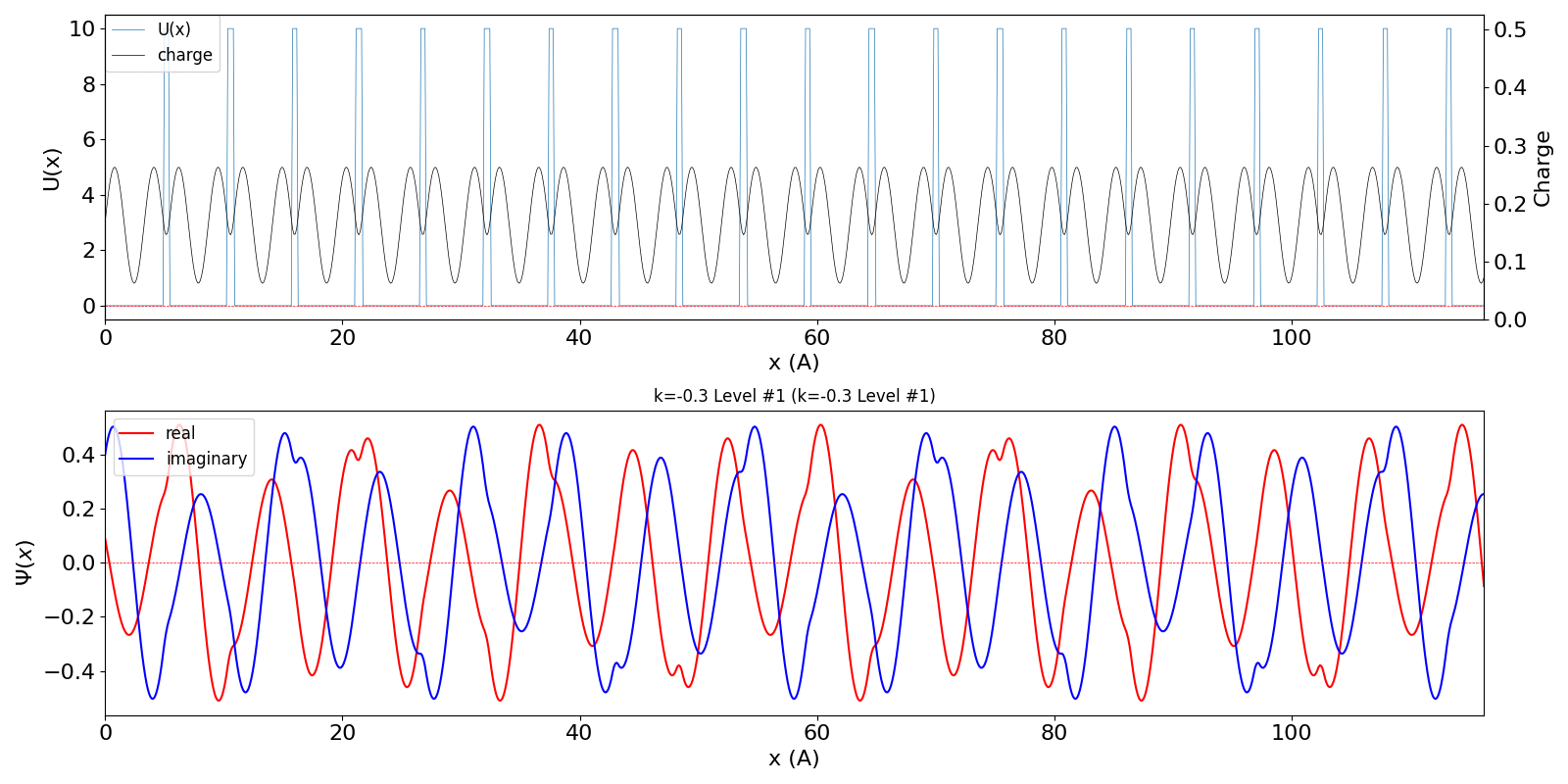
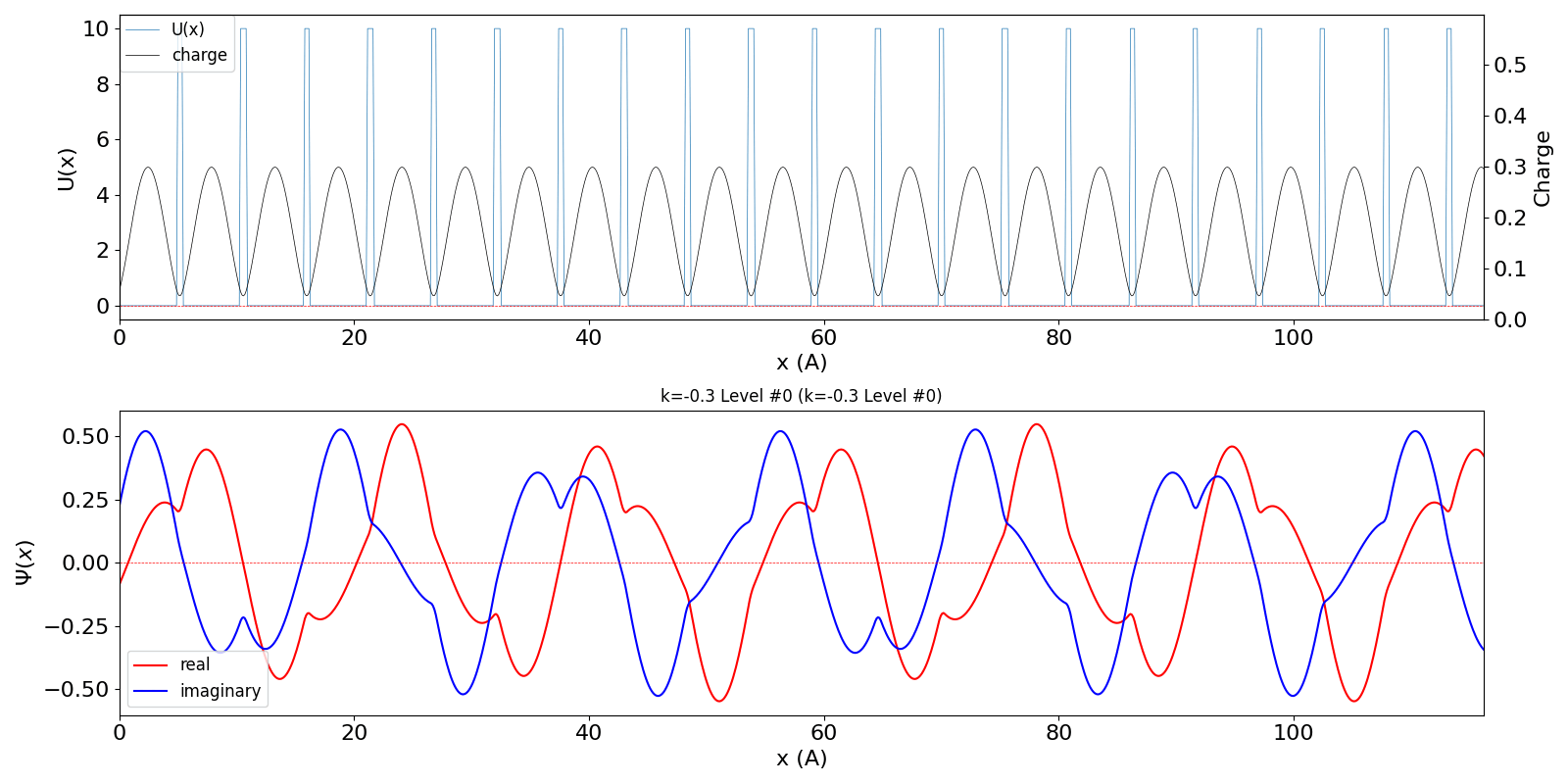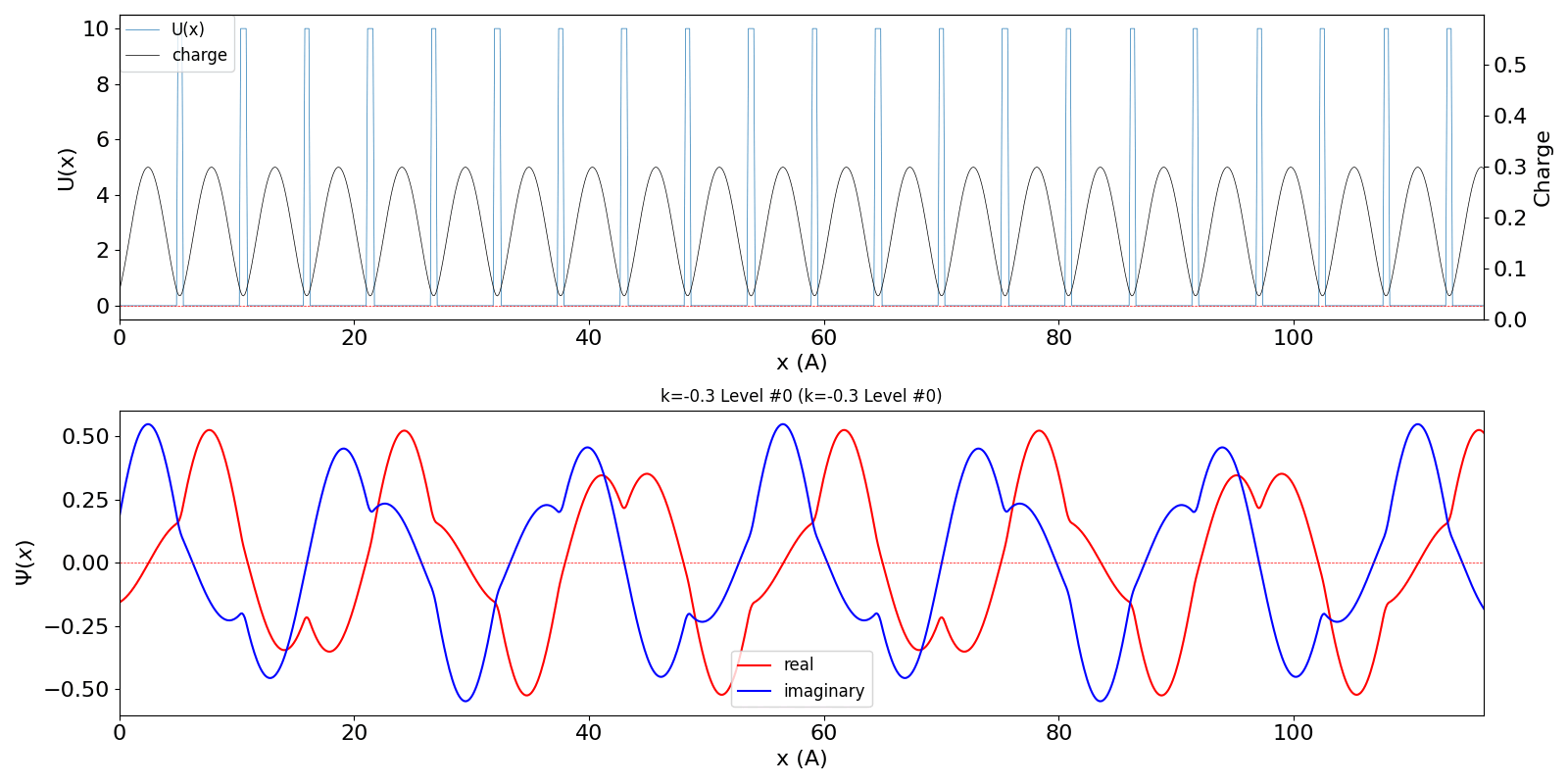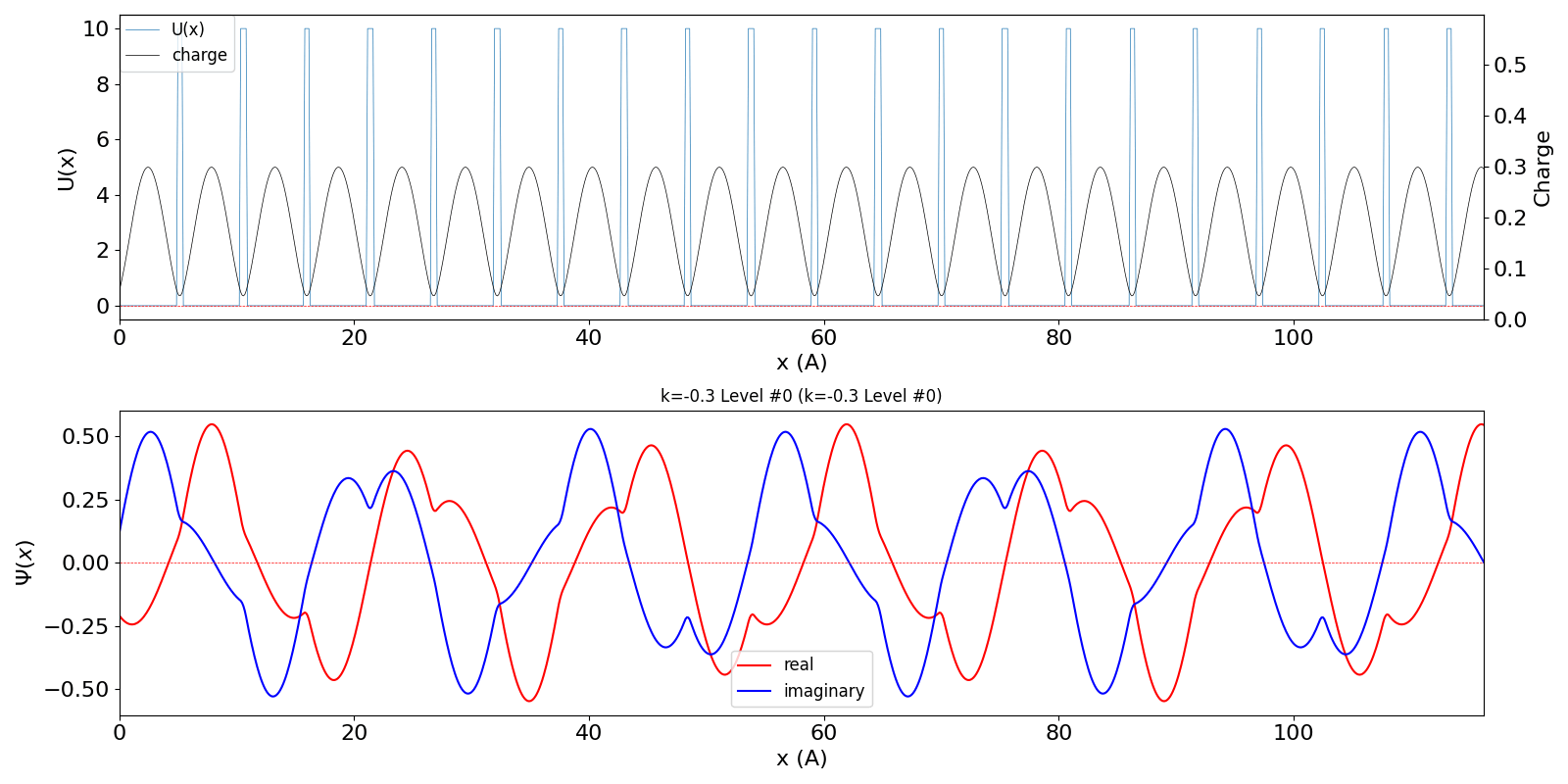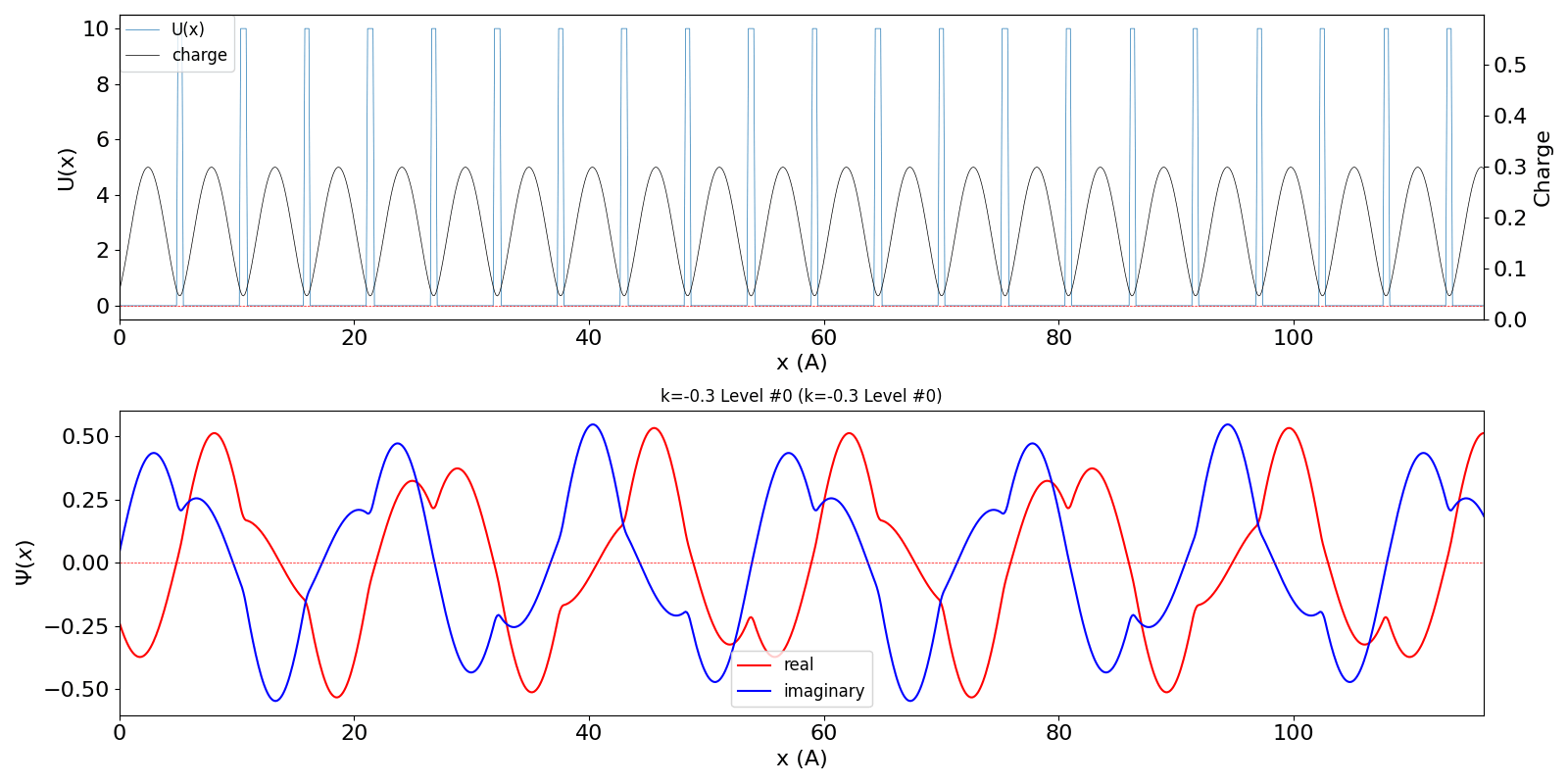
第１BZを超えたBloch波数 kw = 0.7 (左図) は、BZの周期性から kw = -0.3 の第2準位の波動関数 (中図) に一致します。
kronig_penney_wfanim_kw_0.7_Level_0.gif	kronig_penney_wfanim_kw_-0.3_Level_1.gif	kronig_penney_wfanim_kw_-0.3_Level_0.gif